【题目】点P(t,0)是x轴上的动点,Q(0,2t)是y轴上的动点.若线段PQ与函数y=﹣|x|2+2|x|+3的图象只有一个公共点,则t的取值是_____________.
参考答案:
【答案】![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3
或t≤﹣3
【解析】函数y=-|x|2+2|x|+3的解析式可化为:
y=
设线段PQ所在的直线的解析式为:y=kx+b,
将P(t,0)、Q(0,2t)代入得: ![]() ,解得:
,解得: ![]() ,
,
∴线段PQ所在的直线的解析式为:y=-2x+2t;
①当线段PQ过(0,3)时,即点Q与C重合,如图1,
2t=3,t=![]() ,
,
∴当t=![]() 时,线段PQ与函数y=
时,线段PQ与函数y= 只有一个公共点;
只有一个公共点;
当线段PQ过(3,0)时,即点P与A(3,0)重合,如图2,
t=3,
此时线线段PQ与函数y= 有两个公共点,
有两个公共点,
∴当![]() ≤t<3时,线段PQ与函数y=
≤t<3时,线段PQ与函数y= 只有一个公共点;
只有一个公共点;
②将y=-2x+2t代入y=-x2+2x+3(x≥0)中得,
-x2+2x+3=-2x+2t,
-x2+4x+3-2t=0,
△=16-4×(-1)×(3-2t)=28-8t=0,
t=![]() ,
,
∴当t=![]() 时,线段PQ与函数y=
时,线段PQ与函数y= 也只有一个公共点;
也只有一个公共点;
③当线段PQ过B(-3,0),如图3,即P与B(-3,0)重合,线段PQ只与y=-x2-2x+3(x<0)有一个公共点,此时t=-3,
∴当t≤-3时,线段PQ与函数y=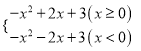 也只有一个公共点;
也只有一个公共点;
综上所述,当线段PQ与函数y=-|x|2+2|x|+3只有一个公共点时,t的取值是![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3,
或t≤﹣3,
故答案为: ![]() ≤t<﹣3或t=
≤t<﹣3或t=![]() 或t≤﹣3.
或t≤﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A
 90°,AB
90°,AB AC.
AC.(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“
 ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB

 PA.
PA.①如图2,点P在△ABC内,∠ABP
 30°,求∠PAB的大小;
30°,求∠PAB的大小;②如图3,点P在△ABC外,连接PC,设∠APC
 α,∠BPC
α,∠BPC β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+
 m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )A. 0 B. 1 C. 2 D. 与m有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
A.( 2,4 )B.( 2,0 )C.( 8,2)D.( 6,0 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的袋子中装有大小、质地完全相同的2个白球和2个黑球.
(1) 先从袋中投出1个球后放回,混合均匀后再摸出1个球,则第一次摸到白球,第二次摸到黑球的概率为P1为__________;
(2) 若第一次从袋子中摸出1个球后不放回,第二次再摸出1个球,则两次摸到的球中有1个白球和1个黑球的概率P2是多少?(请用画树形图或列表法求出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1
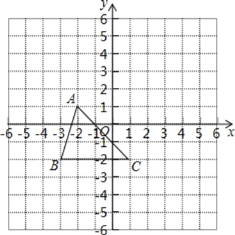
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若直线BC上有一点P,使△PAC的面积是△ABC面积的2倍,直接写出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )

A.2.2米B.2.3米C.2.4米D.2.5米
相关试题

