搜索
【题目】把下列各式因式分解
(1)a(a-3)+2(3-a)
(2) 
(3) 
(4) 
参考答案：
【答案】（1）(a-3)(a-2)（2）4a(b+c)（3）
（4）(2a-b)(2a+b+3)
【解析】试题分析：
（1）先把原式化为
，再用“提公因式法”分解即可；
（2）先用“平方差公式”分解，再提“公因式”即可；
（3）用“完全平方公式”分解即可；
（4）先把原式分组化为
，两组分别分解后，再提“公因式”即可.
试题解析：
（1）a(a-3)+2(3-a)
=a(a-3)-2(a-3)
=(a-3)(a-2) .
（2）
=[（a+b+c）+(a-b-c)][（a+b+c）-(a-b-c)]
=（a+b+c+a-b-c）（a+b+c-a+b+c)
=2a(2b+2c)
=4a(b+c).
（3）
=
=
=
.
（4）
=（
）+（6a-3b）
=(2a+b)(2a-b)+3(2a-b)
=(2a-b)(2a+b+3).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，港口B位于港口A的南偏东
方向，灯塔C恰好在AB的中点处，一艘海轮位于港口A的正南方向，港口B的正西方向的D处，它沿正北方向航行
km，到达E处，测得灯塔C在北偏东
方向上．这时，E处距离港口A有多远？（参考数据： 
）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
过点
， 
． 
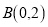为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．（1）求直线AB的解析式和抛物线的解析式；
（2）如果点P是MN的中点，那么求此时点N的坐标；
（3）如果以B，P，N为顶点的三角形与
相似，求点M的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
中， 
， 
， 
，D是AB边的中点，E是AC边上一点，联结DE，过点D作
交BC边于点F，联结EF．（1）如图1，当
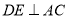时，求EF的长；（2）如图2，当点E在AC边上移动时，
的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出
的正切值；（3）如图3，联结CD交EF于点Q，当
是等腰三角形时，请直接写出BF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DC，连接CF．
（1）如果AB=AC，试猜想四边形ADCF的形状，并证明你的结论；
（2）△ABC满足什么条件时四边形ADCF为正方形，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，三角形纸片ABC中，∠B=2∠C，把三角形纸片沿直线AD折叠，点B落在AC边上的E处，那么下列等式成立的是（ ）
A.AC=AD+BDB.AC=AB+BDC.AC=AD+CDD.AC=AB+CD
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中，BD是一条对角线，点E在直线CD上（与点C，D不重合），连接AE，平移△ADE，使点D移动到点C，得到△BCF，过点F作FG⊥BD于点G，连接AG，EG．
（1）问题猜想：如图1，若点E在线段CD上，试猜想AG与EG的数量关系是____________，位置关系是____________；
（2）类比探究：如图2，若点E在线段CD的延长线上，其余条件不变，小明猜想（1）中的结论仍然成立，请你给出证明；
（3）解决问题：若点E在线段DC的延长线上，且∠AGF=120°，正方形ABCD的边长为2，请在备用图中画出图形，并直接写出DE的长度．
相关试题
