【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)运用待定系数法求解即可;
(2)设![]() ,
, ![]() 得
得![]() ,
, ![]()
再由点坐标公式得出方程,求解即可;
(3)分两种情况进行讨论即可得解.
(1)解:设直线![]() 的解析式为
的解析式为![]() (
(![]() )
)
∵![]() ,
, ![]()
∴![]() 解得
解得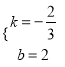
∴直线![]() 的解析式为
的解析式为![]()
∵抛物线![]() 经过点
经过点![]() ,
, ![]()
∴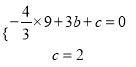 解得
解得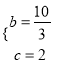
∴![]()
(2)∵![]() 轴,
轴, ![]()
∴设![]() ,
, ![]()
∴![]() ,
, ![]()
∵![]() 点是
点是![]() 的中点
的中点
∴![]()
∴![]()
解得![]() ,
, ![]() (不合题意,舍去)
(不合题意,舍去)
∴![]()
(3)∵![]() ,
, ![]() ,
, ![]()
∴![]() ,
, ![]()
∴![]()
∵![]()
∴当![]() 与
与![]() 相似时,存在以下两种情况:
相似时,存在以下两种情况:
1° ![]()
∴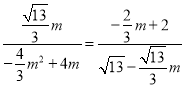 解得
解得![]()
∴![]()
2° ![]()
∴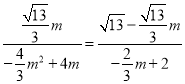 ,解得
,解得![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前
 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:价格
类型
进价(元/盏)
售价(元/盏)
室内用节能灯
40
58
室外用节能灯
50
70
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 分别在
分别在 的边
的边 上运动(不与点
上运动(不与点 重合),
重合), 是
是 的平分线,
的平分线, 的延长线交角
的延长线交角 的平分线于点
的平分线于点 .
.
(1)若
 ,求
,求 的度数.
的度数.(2)若
 ,求
,求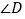 的度数.
的度数.(3)若
 ,请用含
,请用含 的代数式表示
的代数式表示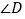 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口B位于港口A的南偏东
 方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行
方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行 km,到达E处,测得灯塔C在北偏东
km,到达E处,测得灯塔C在北偏东 方向上.这时,E处距离港口A有多远?(参考数据:
方向上.这时,E处距离港口A有多远?(参考数据:  )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中,  ,
,  ,
,  ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作 交BC边于点F,联结EF.
交BC边于点F,联结EF.(1)如图1,当
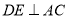 时,求EF的长;
时,求EF的长;(2)如图2,当点E在AC边上移动时,
 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出 的正切值;
的正切值;(3)如图3,联结CD交EF于点Q,当
 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式因式分解
(1)a(a-3)+2(3-a)
(2)

(3)

(4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论;
(2)△ABC满足什么条件时四边形ADCF为正方形,并证明你的结论.

相关试题

