【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

参考答案:
【答案】(1)![]() ;(2)不变;(3)
;(2)不变;(3)![]() 或3或
或3或![]() .
.
【解析】试题分析:(1)由已知条件易求DE=3,DF=4,再由勾股定理EF=5;
(2)过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,由(1)可得DH=3,DG=4;再证
,由(1)可得DH=3,DG=4;再证![]() ,即可得出结论;
,即可得出结论;
(3)分三种情况讨论即可.
(1)∵![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∵![]() 是
是![]() 边的中点
边的中点
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]()
又∵![]()
∴四边形![]() 是矩形
是矩形
∴![]()
∵在![]() 中,
中, ![]()
∴![]()
(2)不变
过点![]() 作
作![]() ,
, ![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]()
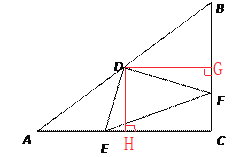
由(1)可得![]() ,
, ![]()
∵![]() ,
, ![]()
∴![]()
又∵![]() ,
,
∴四边形![]() 是矩形
是矩形
∴![]()
∵![]()
∴![]() 即
即![]()
又∵![]()
∴![]()
∴![]()
∵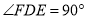
∴![]()
(3)1° 当![]() 时,易证
时,易证![]() ,即
,即![]()
又∵![]() ,D是AB的中点
,D是AB的中点
∴![]()
∴![]()
2° 当![]() 时,易证
时,易证![]()
∵在![]() 中,
中, ![]()
∴设![]() ,则
,则![]() ,
, ![]()
当![]() 时,易证
时,易证![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴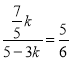 解得
解得![]()
∴![]()
∴![]()
3° 在BC边上截取BK=BD=5,由勾股定理得出![]()
当![]() 时,易证
时,易证![]()
∴设![]() ,则
,则![]() ,
, ![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴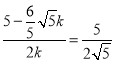 解得
解得![]()
∴![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

-
科目: 来源: 题型:
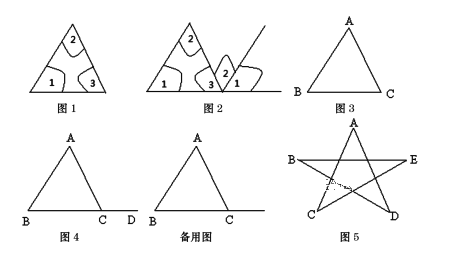
查看答案和解析>>【题目】下列是某初一数学兴趣小组探究三角形内角和的过程,请根据他们的探究过程,结合所学知识,解答下列问题.兴趣小组将图1△ABC三个内角剪拼成图2,由此得△ABC三个内角的和为180度.
(1)请利用图3证明上述结论.
(2)三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角.
如图4,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.
①请探究出∠ACD与∠A、∠B的关系,并直接填空:∠ACD=______.
②如图5是一个五角星,请利用上述结论求∠A+∠B+∠C+∠D+∠E的值.
-
科目: 来源: 题型:
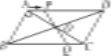
查看答案和解析>>【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
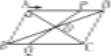 备用图
备用图 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y1=
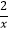 (x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=
(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2= 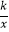 (k<0,x<0)的图象于点B.
(k<0,x<0)的图象于点B.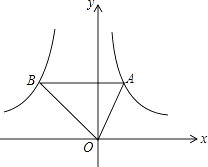
(1)若S△AOB的面积等于3,则k是=;
(2)当k=﹣8时,若点A的横坐标是1,求∠AOB的度数;
(3)若不论点A在何处,反比例函数y2=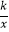 (k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
(k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题:
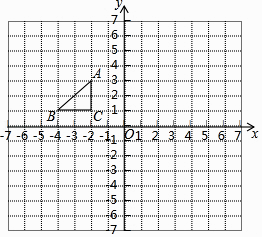
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长.
相关试题

