【题目】若二次函数y=x2﹣2x+2在自变量x满足m≤x≤m+1时的最小值为6,则m的值为( )
A. ![]() B.
B. ![]()
C. 1D. ![]()
参考答案:
【答案】B
【解析】
由抛物线解析式确定出其对称轴为x=1,分m>1或m+1<1两种情况,分别确定出其最小值,由最小值为6,则可得到关于m的方程,可求得m的值.
∵y=x2﹣2x+2=(x﹣1)2+1,
∴抛物线开口向上,对称轴为x=1,
当m>1时,可知当自变量x满足m≤x≤m+1时,y随x的增大而增大,
∴当x=m时,y有最小值,
∴m2﹣2m+2=6,解得m=1+![]() 或m=1﹣
或m=1﹣![]() (舍去),
(舍去),
当m+1<1时,可知当自变量x满足m≤x≤m+1时,y随x的增大而减小,
∴当x=m+1时,y有最小值,
∴(m+1)2﹣2(m+1)+2=6,解得m=![]() (舍去)或m=﹣
(舍去)或m=﹣![]() ,
,
综上可知m的值为1+![]() 或﹣
或﹣![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
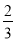 ,3)在反比例函数C:y=
,3)在反比例函数C:y=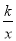 (x>0)上,点P是反比例函数C:y=
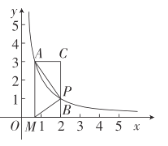
(x>0)上,点P是反比例函数C:y=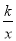 (x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.(1)求反比例函数的解析式;
(2)若点P(2,n),求PM所在直线的解析式;
(3)PB⊥x轴,B为垂足,CA⊥y轴,BP的延长线交AC于点C,当△AMP与△APC相似时,请写出∠AMP与∠BMP的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=2x2+4x+k﹣1(k为大于2的正整数)与x轴有交点.
(1)求k的值及抛物线y=2x2+4x+k﹣1的对称轴;
(2)将抛物线y=2x2+4x+k﹣1在直线y=2上方的部分沿直线y=2翻折,其余部分不变,得到一个新图象,当直线y=
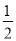 x+b与此图象有两个公共点时,求b的取值范围.
x+b与此图象有两个公共点时,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,DC=8,现将四边形BEGC沿折痕EG(G,E分别在DC,AB边上)折叠,其顶点B,C分别落在边AD上和边DC的上部,其对应点设为F,N点,且FN交DC于M.
特例体验:
(1)当FD=AF时,△FDM的周长是多少?
类比探究:
(2)当FD≠AF≠0时,△FDM的周长会发生变化吗?请证明你的猜想.
拓展延伸:
(3)同样在FD≠AF≠0的条件下,设AF为x,被折起部分(即:四边形FEGN)的面积为S,试用含x的代数式表示S,并问:当x为何值时,S=26?
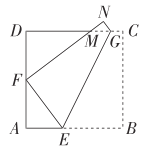
-
科目: 来源: 题型:
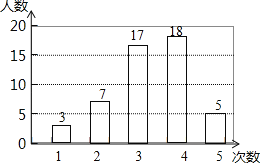
查看答案和解析>>【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
(1)这50个样本数据的中位数是 次,众数是 次;
(2)求这50个样本数据的平均数;
(3)根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地如图,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数图象;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数图象;请根据图象解答下到问题:
(1)货车离甲地距离y(干米)与时间x(小时)之间的函数式为 ;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中A(5,0),B为y轴上任意一点,以点B为直角顶点作等腰Rt△ABC(点A、B、C按顺时针方向排列),请探究点C是否在一确定的直线上;
(2)在平面直角坐标系中,A(﹣1,0),B(4,2m),连接AB,将AB绕点B逆时针旋转90°到CB,请探究点C是否在一确定的直线上.
相关试题

