【题目】已知抛物线y=2x2+4x+k﹣1(k为大于2的正整数)与x轴有交点.
(1)求k的值及抛物线y=2x2+4x+k﹣1的对称轴;
(2)将抛物线y=2x2+4x+k﹣1在直线y=2上方的部分沿直线y=2翻折,其余部分不变,得到一个新图象,当直线y=![]() x+b与此图象有两个公共点时,求b的取值范围.
x+b与此图象有两个公共点时,求b的取值范围.
参考答案:
【答案】(1)k=3;x=﹣1;(2)2<b<3或b<![]()
【解析】
(1)令y=0,由一元二次方程根的判别式,即可求出k的取值范围,庵后得到k的值;由抛物线的对称轴公式,即可求出对称轴;
(2)根据题意,画出翻折后的图形,然后找出有两个函数有两个交点的临界点,求出临界点是b的值,然后即可得到b的取值范围.
解:(1)∵抛物线y=2x2+4x+k-1与x轴有交点,
∴42-4![]() 2(k-1)=24-8k≥0,
2(k-1)=24-8k≥0,
解得:k≤3,
∵k为大于2的正整数,
∴k=3.
∴抛物线的解析式为:y=2x2+4x+2,
其对称轴为:x=﹣![]() =﹣1;
=﹣1;
(2)将抛物线y=2x2+4x+2在直线y=2上方的部分沿直线y=2翻折,
得到的图象的解析式为:y=﹣2(x+1)2+4,
依题意可作翻折后的图象如图所示.
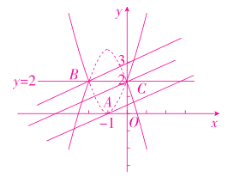
由图象可知,直线y=![]() x+b与新图象有两个交点,包括如下两种情况:
x+b与新图象有两个交点,包括如下两种情况:
①应使直线在点(﹣1,0)的下方,当直线y=![]() x+b经过点A(﹣1,0)时,
x+b经过点A(﹣1,0)时,
可得b=![]() ,此时b<
,此时b<![]() ,直线y=
,直线y=![]() x+b与新图象有两个交点.
x+b与新图象有两个交点.
②当直线y=![]() x+b经过点B(﹣2,2)时,
x+b经过点B(﹣2,2)时,
可得b=3;
当直线y=![]() x+b经过点C(O,2)时,可得b=2
x+b经过点C(O,2)时,可得b=2
由图象可知,符合题意的b的取值范围为:2<b<3或b<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,对角线AC与BD交于点P,下面给出5个论断:①AB//CD;②AP=PC;③AB=CD;④∠BAD=∠DCB;⑤AD//BC.
(1)若用论断①和④作为条件,试证四边形ABCD是矩形.
(2)请你另选取两个能推出四边形ABCD为矩形的论断.如:_________和_________、___________和________________(不证明,用序号表示即可).
(3)若选取论断③和⑤作为条件,能推出四边形ABCD为矩形吗?若能,请给出证明;若不能,请举反例说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6m 长的圆钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪长为 0.8m 的用料时,最多可剪 根;
方法②:当先剪下 1 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根;
方法③:当先剪下 2 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根.
(2)分别用(1)中的方法②和方法③各裁剪多少根 6m 长的钢管,才能刚好得到所需要的相应数量的材料?
(3)试探究:除(2)中方案外,在(1)中还有哪两种方法联合,所需要 6m 长的钢管与(2) 中根数相同?
-
科目: 来源: 题型:
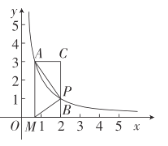
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
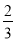 ,3)在反比例函数C:y=
,3)在反比例函数C:y=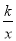 (x>0)上,点P是反比例函数C:y=
(x>0)上,点P是反比例函数C:y=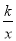 (x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.(1)求反比例函数的解析式;
(2)若点P(2,n),求PM所在直线的解析式;
(3)PB⊥x轴,B为垂足,CA⊥y轴,BP的延长线交AC于点C,当△AMP与△APC相似时,请写出∠AMP与∠BMP的数量关系,并说明理由.
-
科目: 来源: 题型:
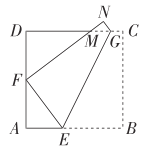
查看答案和解析>>【题目】如图,在正方形ABCD中,DC=8,现将四边形BEGC沿折痕EG(G,E分别在DC,AB边上)折叠,其顶点B,C分别落在边AD上和边DC的上部,其对应点设为F,N点,且FN交DC于M.
特例体验:
(1)当FD=AF时,△FDM的周长是多少?
类比探究:
(2)当FD≠AF≠0时,△FDM的周长会发生变化吗?请证明你的猜想.
拓展延伸:
(3)同样在FD≠AF≠0的条件下,设AF为x,被折起部分(即:四边形FEGN)的面积为S,试用含x的代数式表示S,并问:当x为何值时,S=26?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=x2﹣2x+2在自变量x满足m≤x≤m+1时的最小值为6,则m的值为( )
A.
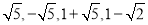 B.
B. 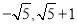
C. 1D.
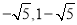
-
科目: 来源: 题型:
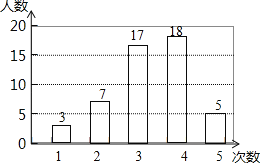
查看答案和解析>>【题目】在开展“学雷锋社会实践”活动中,某校为了解全校1000名学生参加活动的情况,随机调查了50名学生每人参加活动的次数,并根据数据绘成如图的条形统计图:
(1)这50个样本数据的中位数是 次,众数是 次;
(2)求这50个样本数据的平均数;
(3)根据样本数据,估算该校1000名学生大约有多少人参加了4次实践活动.
相关试题

