【题目】在下列条件中:①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶5∶6,③∠A=90°-∠B,④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有 ( )
∠C中,能确定△ABC是直角三角形的条件有 ( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
根据三角形的内角和等于180°分别求出各小题中的最大角的度数,即可得解.
解:①∵∠A+∠B=∠C,
∴∠A+∠B+∠C=2∠C=180°,
∴∠C=90°,
故正确;
②∵∠A:∠B:∠C=1:5:6,
∴最大角∠C=180°×![]() =90°,
=90°,
故正确;
③∵∠A=90°﹣∠B,
∴∠A+∠B=90°,
∴∠C=180°﹣90°=90°,
故正确;
④∵∠A=∠B=![]() ∠C,
∠C,
∴∠A+∠B+∠C=![]() ∠C+
∠C+![]() ∠C+∠C=2∠C=180°,
∠C+∠C=2∠C=180°,
∴∠C=90°,
故正确;
综上所述,是直角三角形的是①②③④共4个.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试证明∠BOC=90°+
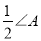
(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(3)如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
-
科目: 来源: 题型:
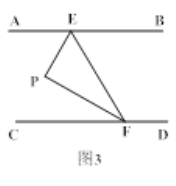
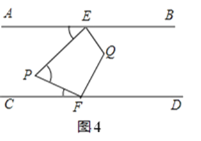
查看答案和解析>>【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.
(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为 ,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为 .
(2)如图3,当∠EPF=90°,FP平分∠EFC时,求证:EP平分∠AEF;
(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF= .
②猜想∠EPF与∠EQF的数量关系,并说明理由;
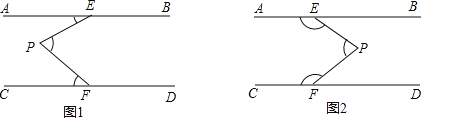
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结矩形四边中点所得的四边形一定是( )
A.菱形
B.矩形
C.正方形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是AE=1,CF=2,则EF长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在平面直角坐标系中,对
 进行循环往复的轴对称变换,若原来点A坐标是
进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是________.
,则经过第2019次变换后所得的A点坐标是________.
-
科目: 来源: 题型:
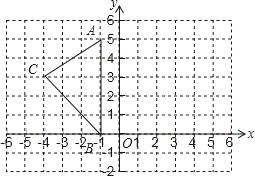
查看答案和解析>>【题目】如图:在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)S△ABC= .
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1(其中点A、B、C的对称点分别为点A1、B1、C1).
(3)写出点A1、B1、C1的坐标.A1 ,B1 ,C1 .
相关试题

