【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )

参考答案:
【答案】见解析
【解析】
根据三角形内角和定理以及平行线的性质即可求出答案.
证明:∵AD⊥BC,EF⊥BC( 已知),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥AD( 同位角相等,两直线平行)
∴∠1=∠3( 两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠2=∠3(等量代换)
∴DG∥AB(内错角相等,两直线平行)
故答案为:已知;AD;同位角相等,两直线平行;∠3;两直线平行,同位角相等;∠2=∠3;等量代换;内错角相等,两直线平行;
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( )
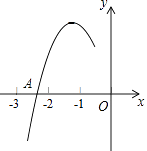
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
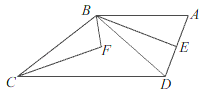
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
A. 115° B. 110° C. 105° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数
3
4
5
6
……
18
∠α的度数
……
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.
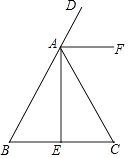
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.
相关试题

