【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
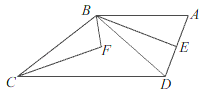
A. 115° B. 110° C. 105° D. 100°
参考答案:
【答案】D
【解析】
依据四边形BCDE的内角和,可得∠BCD+∠CBE=160°,再根据∠EBC和∠DCB的角平分线相交于点F,可得∠BCF+∠CBF=![]() ×160°=80°,进而得出△BCF中,∠F=180°-80°=100°.
×160°=80°,进而得出△BCF中,∠F=180°-80°=100°.
解:∵BE⊥AD,
∴∠BED=90°,
又∵∠ADC=110°,
∴四边形BCDE中,∠BCD+∠CBE=360°-90°-110°=160°,
又∵∠EBC和∠DCB的角平分线相交于点F,
∴∠BCF+∠CBF=![]() ×160°=80°,
×160°=80°,
∴△BCF中,∠F=180°-80°=100°,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A与A′重合,若∠A=α,则∠1+∠2=( )
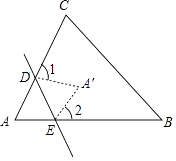
A.α
B.2α
C.180°﹣α
D.180°﹣2α -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=_____.
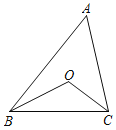
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列4个结论::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④点M(x1 , y1)、N(x2 , y2)在抛物线上,若x1<x2 , 则y1≤y2 , 其中正确结论的个数是( )
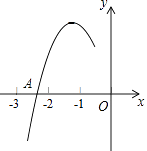
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,E为AB边上任意一点,EF⊥BC于点F,∠1=∠2.求证:DG∥AB.请把证明的过程填写完整.
证明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定义)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.

相关试题

