搜索
【题目】如图，在四边形ABCD中，已知AB=4cm，BC=3cm，AD=12cm，DC=13cm，∠B=90°，求四边形ABCD的面积。
参考答案：
【答案】解：连接AC，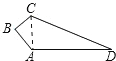
∵∠B=90°
∴AC2=AB2+BC2=16+9=25
∵AD2=144，DC2=169
∴AC2+AD2=DC2
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=
×3×4+×12×5=36cm
【解析】连接AC，先根据直角三角形的性质得到AC边的长度，再根据三角形ACD中的三边关系可判定△ACD是Rt△，把四边形分成两个直角三角形即可求得面积．
【考点精析】本题主要考查了勾股定理的逆定理的相关知识点，需要掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x2﹣8x+20=0的根的情况是（ ）
A. 没有实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 有两个不相等的实数根
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，以AB为直径的⊙O分别于BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F．
（1）求证：DF⊥AC；
（2）若⊙O的半径为5，∠CDF=30°，
求
长（结果保留π）．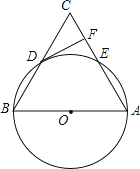 
-
科目： 来源： 题型：
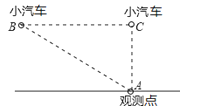
查看答案和解析>>【题目】省道S226在我县境内某路段实行限速，机动车辆行驶速度不得超过60km/h，如图，一辆小汽车在这段路上直道行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方36m的C处，过了3s后，测得小汽车与车速检测仪间距离为60m，这辆小汽车超速了吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】不论x，y为任何实数，x2+y2﹣4x﹣2y+8的值总是（ ）
A.正数
B.负数
C.非负数
D.非正数 -
科目： 来源： 题型：
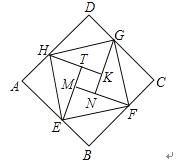
查看答案和解析>>【题目】如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 ． 若S1+S2+S3=15，则S2的值是（ ）
A.3
B.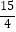
C.5
D.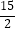
? -
科目： 来源： 题型：
查看答案和解析>>【题目】若多项式2x2－3x＋6的值为8，则多项式9－4x2＋6x的值是( )
A. 13 B. 11 C. 5 D. －7
相关试题
