【题目】如图1,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() .
.
(1)求点A、B的坐标;
(2)如图1,P点为y轴正半轴上一点,连接BP,若![]() ,请求出P点的坐标;
,请求出P点的坐标;
(3)如图2,已知![]() ,若C点是x轴上一个动点,是否存在点C,使
,若C点是x轴上一个动点,是否存在点C,使![]() ,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.
,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,![]() ,理由见解析
,理由见解析
【解析】
(1)首先根据等式,可得出![]() 和
和![]() 的值,即可得出点A、B的坐标;
的值,即可得出点A、B的坐标;
(2)首先作![]() 轴于点M,设
轴于点M,设![]() ,且
,且![]() ,利用
,利用![]() ,列出等式,即可得出点P的坐标;
,列出等式,即可得出点P的坐标;
(3)根据题意,利用等腰三角形的性质,即可直接判定C的坐标,有两种情况,在x正半轴和负半轴上,即可得解.
解:(1)![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
(2)作![]() 轴于点M,如图所示
轴于点M,如图所示
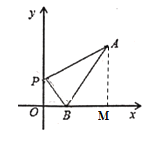
设![]() ,且
,且![]()
∴![]()
![]()
若![]()
即![]()
∴![]()
∴![]()
(3)存在,![]() ,
,![]()
∵![]() ,
,![]() ,
,![]()
∴当C点在x正半轴上时,坐标为![]() ,
,
当C点在x负半轴上时,坐标为![]()
故答案为![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 分别在
分别在 上,
上, 如图1.若
如图1.若 ,且
,且 ,求
,求

 如图2,若
如图2,若 . 求证:
. 求证: 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出
 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料
材料一:对于任意的非零实数
 和正实数
和正实数 ,如果满足
,如果满足 为整数,则称k是x的一个整商系数,
为整数,则称k是x的一个整商系数,例如:当
 时,
时, ,则称
,则称 是
是 的一个整商系数;
的一个整商系数;当
 时,
时, ,则称
,则称 是
是 的一个整商系数;
的一个整商系数;当
 时,
时, ,则称
,则称 是
是 的一个整商系数;
的一个整商系数;给论:一个非零实数
 有无数个整商系数
有无数个整商系数 ,其中最小的一个整商系数记为
,其中最小的一个整商系数记为 ;
;例如:
 ,
,材料二:对于一元二次方程
 的两根
的两根 ,有如下关系:
,有如下关系:
请根据材料解决下列问题


 若关于
若关于 的方程:
的方程:的两根分别为  ,且满足
,且满足 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
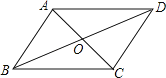
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
相关试题

