【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.
(1)求点E的坐标;
(2)求△OPE的周长.

参考答案:
【答案】(1)点E的坐标是(4,2);
(2)△OPE的周长为![]() .
.
【解析】(1)过点E作EM⊥y轴于点M,根据面积公式EM=4,根据正方形性质求出CM=ME=4,即可求出答案;
(2)根据全等求出BE=OE,求出直线BE的解析式,求出P的坐标,根据勾股定理求出BP,即可求出答案.
解:(1)过点E作EM⊥y轴于点M,
∴![]() OCEM=12,
OCEM=12,

即![]() ×6×EM=12, ∴EM=4,
×6×EM=12, ∴EM=4,
∵四边形OABC是正方形,∴∠MCE=45°,
∴△MEC是等腰直角三角形, ∴MC=ME=4,
∴MO=6﹣4=2,
∴点E的坐标是(4,2);
(2)设直线BE的解析式为y=kx+b,
把B(6,6)和点E(4,2)的坐标代入函数解析式得: ![]() ,
,
解得:k=2,b=﹣6,
∴直线BE的解析式为y=2x﹣6,
令2x﹣6=0得:x=3,
∴点P的坐标为(3,0),∴OP=3,
∵四边形ABCO是正方形,
∴OC=CB,∠BCE=∠OCE,
在△OCE和△BCE中,
OC=BC,∠OCE=∠BCE,CE=CE,
∴△OCE≌△BCE(SAS),
∴OE=BE,
在Rt△PBA中,由勾股定理可得:PB=![]() =3
=3![]() ,
,
∴C△OPE =OE+PE+OP=3+PB=3+3![]() .
.
“点睛”本题考查了正方形的性质,坐标与图形性质,用待定系数法求出一次函数的解析式,勾股定理等知识点,能综合运用知识点进行计算是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )

A.(
 )米 B.12米 C.(
)米 B.12米 C.( )米 D.10米
)米 D.10米 -
科目: 来源: 题型:
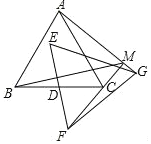
查看答案和解析>>【题目】如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
A.2-
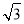 B.
B.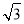 +1 C.
+1 C.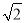 D.
D.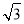 -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:x(2x-y)-(x+y) (x-y) + (x-y) 2,其中x2+y2=5,xy=-2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若分解因式2x2+mx+15=(x-5)(2x-3),则( )
A. m=-7 B. m=7 C. m=-13 D. m=13
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个n边形的内角和是720°,那么n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=
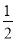 x2-3x+
x2-3x+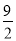 交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).
交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).(1)当k=2,b=-3
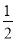 时,求A,D两点坐标;
时,求A,D两点坐标;(2)当b=2-3k时,直线AD交抛物线的对称轴于点P,交线段CE于点F,求
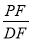 的最小值;
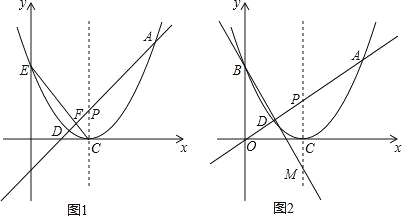
的最小值;(3)当b=0时,若B是抛物线上点A的对称点,直线BD交对称轴于点M,求证:PC=CM.
相关试题

