【题目】先化简,再求值:x(2x-y)-(x+y) (x-y) + (x-y) 2,其中x2+y2=5,xy=-2 .
参考答案:
【答案】16
【解析】分析:原式利用单项式乘以多项式,平方差公式,完全平方公式化简,去括号合并得到最简结果,把已知等式代入计算即可求出值.
详解:原式=2x2﹣xy﹣x2+y2+x2﹣2xy+y2
=2x2+2y2﹣3xy,
当x2+y2=5,xy=﹣2时,原式=2×5﹣3×(﹣2)=10+6=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A. (﹣2,0)B. (﹣2,﹣1)C. (﹣1,﹣1)D. (﹣1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )

A.(
 )米 B.12米 C.(
)米 B.12米 C.( )米 D.10米
)米 D.10米 -
科目: 来源: 题型:
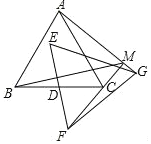
查看答案和解析>>【题目】如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是( )
A.2-
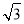 B.
B.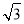 +1 C.
+1 C.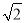 D.
D.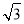 -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.
(1)求点E的坐标;
(2)求△OPE的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若分解因式2x2+mx+15=(x-5)(2x-3),则( )
A. m=-7 B. m=7 C. m=-13 D. m=13
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个n边形的内角和是720°,那么n= .
相关试题

