Question

【题目】给出下列定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形，下列说法：
①如图①，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点，则中点四边形EFGH是平行四边形．
②如图②，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，则中点四边形EFGH是菱形
③在（2）中增加条件∠APB=∠CPD=90°，其他条件不变，则中点四边形EFGH是正方形
其中，正确的有（ ）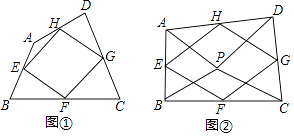

A.0个
B.1个
C.2个
D.3个

Answer 1

【答案】D
【解析】解：如图①，连接AC，BD，

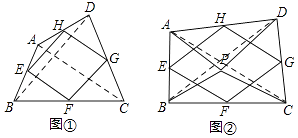
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点，

∴EF=HG= AC，EH=FG= BD，

∴四边形EFGH是平行四边形，故（1）正确；

如图②，连接AC，BD，

∵PA=PB，PC=PD，∠APB=∠CPD，

∴∠BPD=∠APC，

∴△BPD≌△APC，

∴AC=BD，

∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点，

∴EF=HG= AC=EH=FG= BD，

∴四边形EFGH是菱形，故（2）正确；

在（2）中增加条件∠APB=∠CPD=90°，其他条件不变，

由△BPD≌△APC，可得∠CAP=∠DBP，

∵△ABP中，∠PAB+∠ABD+∠DBP=90°，

∴∠PAB+∠ABD+∠CAP=90°，

∴AC⊥BD，

由点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点，可得EH∥BD，EF∥AC，

∴EH⊥EF，

即∠HEF=90°，

∴菱形EFGH是正方形，故（3）正确，

所以答案是：D．