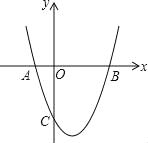
【题目】如图,抛物线y=![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
参考答案:
【答案】(1) y=![]() ﹣2x﹣3;(2)①证明详见解析;②△AEF是等腰直角三角形,理由详见解析.
﹣2x﹣3;(2)①证明详见解析;②△AEF是等腰直角三角形,理由详见解析.
【解析】
试题分析:(1)将A、B、C三点坐标代入抛物线方程,即可求得a、b、c的值;
(2)①由B、C、D三点的坐标即可得出∠CBO=∠OBD=45°,从而得出∠EBF=90°,即可得出EF为圆的直径;
②利用同圆内,同弧所对的圆周角相等,可以找到∠AEF=∠AFE=45°,从而得出△AEF是等腰直角三角形.
试题解析:(1)∵抛物线y=![]() +bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
∴ ,解得
,解得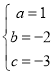 ,
,
∴抛物线的解析式为y=![]() ﹣2x﹣3;
﹣2x﹣3;
(2)按照题意画出图形,如下图,
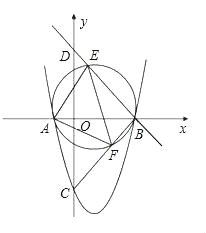
①∵B点坐标(3,0)、C点坐标(0,﹣3),
∴OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
又∵D是y轴正半轴上的点,OD=3,
∴△BOD为等腰直接三角形,
∴∠OBD=45°,
∠CBD=∠CBO+∠OBD=45°+45°=90°,
即∠FBE=90°,
∴EF是圆的直径.
②∵∠CBO=∠OBD=45°,∠AFE=∠OBD,∠AEF=∠CBO(在同圆中,同弧所对的圆周角相等),
∴∠AEF=∠AFE=45°,
∴∠FAE=90°,AE=AF,
∴△AEF是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=5,xy=2,则(x+2)(y+2)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1与∠2互补,∠3与30°互余,∠2+∠3=210°,则∠1=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a﹣4)(a﹣2)=3,则(a﹣4)2+(a﹣2)2的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A,B的速度比是1:4.(速度单位:单位长度/秒)
(1)求出两个动点运动的速度,并在数轴上标出A,B两点从原点出发运动3秒时的位置;
(2)若A,B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;
(3)在(2)中A,B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】若2a2+b2﹣2ab﹣6a≤﹣9,则ab=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:|3﹣xy|+(x+y﹣2)2=0,求x2+y2+4xy的值.
相关试题

