搜索
【题目】若∠1与∠2互补，∠3与30°互余，∠2+∠3=210°，则∠1=度．
参考答案：
【答案】30
【解析】解：∵∠3与30°互余， ∴∠3=90°﹣30°=60°，
∵∠2+∠3=210°，
∴∠2=150°，
∵∠1与∠2互补，
∴∠1+∠2=180°，
∴∠1=30°．
所以答案是：30．
【考点精析】根据题目的已知条件，利用余角和补角的特征的相关知识可以得到问题的答案，需要掌握互余、互补是指两个角的数量关系，与两个角的位置无关．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，AD是BC边上的高，BD=3，CD=1，AD=2，P、Q、R分别是BC、AB、AC边上的动点，则△PQR周长的最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某呼吸机制造商2020年一月份生产呼吸机1000台，2020年三月份生产呼吸机4000台，设二、三月份每月的平均增长率为x，根据题意，可列方程为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知x+y=5，xy=2，则（x+2）（y+2）= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知（a﹣4）（a﹣2）=3，则（a﹣4）2+（a﹣2）2的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=
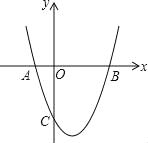
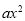+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C（0，﹣3）．（1）求抛物线的解析式；
（2）D是y轴正半轴上的点，OD=3，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，
①试说明EF是圆的直径；
②判断△AEF的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A，B的速度比是1：4．（速度单位：单位长度/秒）
（1）求出两个动点运动的速度，并在数轴上标出A，B两点从原点出发运动3秒时的位置；
（2）若A，B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；
（3）在（2）中A，B两点继续同时向数轴负方向运动时，另一动点C同时从B点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．
相关试题
