【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 
参考答案:
【答案】![]()
【解析】解:∵四边形ABCD为正方形,点O是对角线的交点,
∴∠MBO=∠NCO=45°,OB=OC,∠BOC=90°,
∵∠MON=90°,
∴∠MOB+∠BON=90°,∠BON+∠NOC=90°,
∴∠MOB=∠NOC.
在△MOB和△NOC中,有 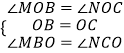 ,
,
∴△MOB≌△NOC(ASA).
同理可得:△AOM≌△BON.
∴S阴影=S△BOC= ![]() S正方形ABCD .
S正方形ABCD .
∴蚂蚁停留在阴影区域的概率P= ![]() =
= ![]() .
.
故答案为: ![]() .
.
根据正方形的性质可得出“∠MBO=∠NCO=45°,OB=OC,∠BOC=90”,通过角的计算可得出∠MOB=∠NOC,由此即可证出△MOB≌△NOC,同理可得出△AOM≌△BON,从而可得知S阴影= ![]() S正方形ABCD , 再根据几何概率的计算方法即可得出结论.本题考查了几何概率.正方形的性质以及全等三角形的判断及性质,解题的关键是找出S阴影=S△BOC=
S正方形ABCD , 再根据几何概率的计算方法即可得出结论.本题考查了几何概率.正方形的性质以及全等三角形的判断及性质,解题的关键是找出S阴影=S△BOC= ![]() S正方形ABCD . 本题属于基础题,难度不大,解决该题型题目时,根据正方形的性质和角的计算找出相等的边角关系,再利用全等三角形的判定定理证出三角形全等是关键.
S正方形ABCD . 本题属于基础题,难度不大,解决该题型题目时,根据正方形的性质和角的计算找出相等的边角关系,再利用全等三角形的判定定理证出三角形全等是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E、F分别是△ABC各边中点,若AB=AC=10,BC=12,求四边形ADEF的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交边AB于G.
(1)线段AF与GB相等吗?
(2)当四边形ABCD满足什么条件时,△EFG为等腰直角三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD∥BC,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?

-
科目: 来源: 题型:
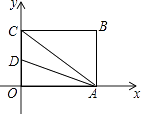
查看答案和解析>>【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为 .
相关试题

