【题目】如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为 . 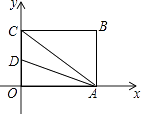
参考答案:
【答案】(0, ![]() )
)
【解析】解:过D作DE⊥AC于E, 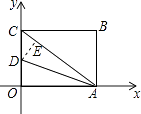
∵四边形ABCO是矩形,B(4,3),
∴OC=AB=3,OA=BC=4,∠CCOA=90°,
∵AD平分∠OAC,
∴OD=DE,
由勾股定理得:OA2=AD2﹣OD2 , AE2=AD2﹣DE2 ,
∴OA=AE=4,
由勾股定理得:AC= ![]() =5,
=5,
在Rt△DEC中,DE2+EC2=CD2 ,
即OD2+(5﹣4)2=(3﹣OD)2 ,
解得:OD= ![]() ,
,
所以D的坐标为(0, ![]() ),
),
故答案为:(0, ![]() ).
).
过D作DE⊥AC于E,根据矩形的性质和B的坐标求出OC=AB=3,OA=BC=4,∠CCOA=90°,求出OD=DE,根据勾股定理求出OA=AE=4,AC=5,在Rt△DEC中,根据勾股定理得出DE2+EC2=CD2 , 求出OD,即可得出答案.本题考查了矩形的性质,角平分线性质,勾股定理的应用,能根据勾股定理得出关于OD的方程是解此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交边AB于G.
(1)线段AF与GB相等吗?
(2)当四边形ABCD满足什么条件时,△EFG为等腰直角三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD∥BC,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动.
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2
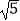 ,反比例函数y=
,反比例函数y= 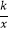 的图象经过点B,则k的值为 .
的图象经过点B,则k的值为 . 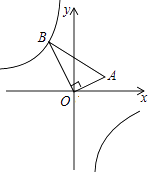
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y=
 x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=  x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示) 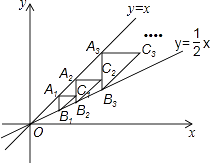
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=3,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是()

A. △BPQ是等边三角形 B. △PCQ是直角三角形 C. ∠APB=150° D. ∠APC=135°
相关试题

