Question

【题目】如图，在△ABC中，∠C=90°，∠B=32°，以A为圆心，任意长为半径画弧分别交AB ， AC于点M和N ， 再分别以M ， N为圆心，大于 MN的长为半径画弧，两弧交于点P ， 连接AP并延长交BC于点D ， 则下列说法：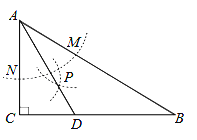
①AD是∠BAC的平分线；
②CD是△ADC的高；
③点D在AB的垂直平分线上；
④∠ADC=61°．
其中正确的有（　　）
A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】C
【解析】根据作法可得AD是∠BAC的平分线，故①正确； ∵∠C=90°，
∴CD是△ADC的高，故②正确；
∵∠C=90°，∠B=32°，
∴∠CAB=58°，
∵AD是∠BAC的平分线，
∴∠CAD=∠DAB=29°，
∴AD≠BD ，
∴点D不在AB的垂直平分线上，故③错误；
∵∠CAD=29°，∠C=90°，
∴∠CDA=61°，故④正确；
共有3个正确，
选C．