【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC. 证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°
∴∠ADC=∠EGC(等量代换)
∴AD∥EG
∴∠1=∠3
∠2=∠E
又∵∠E=∠3( 已知)
∴∠1=∠2
∴AD平分∠BAC . 
参考答案:
【答案】(垂直的定义);(同位角相等,两直线平行);(两直线平行,内错角相等);(两直线平行,同位角相等);(等量代换);(角平分线的定义)
【解析】证明:∵AD⊥BC于D,EG⊥BC于G( 已知 ), ∴∠ADC=90°,∠EGC=90° (垂直的定义),
∴∠ADC=∠EGC(等量代换),
∴AD∥EG(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
∠2=∠E(两直线平行,同位角相等),
又∵∠E=∠3( 已知),
∴∠1=∠2 (等量代换),
∴AD平分∠BAC,
所以答案是:(垂直的定义);(同位角相等,两直线平行);(两直线平行,内错角相等);(两直线平行,同位角相等);(等量代换);(角平分线的定义).
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a+2)2+|b﹣1|=0,则(b+a)2015= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形具有而菱形不一定具有性质的是( )
A. 对角线互相平分 B. 对角线相等
C. 对角线平分一组对角 D. 对角线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB , AC于点M和N , 再分别以M , N为圆心,大于
 MN的长为半径画弧,两弧交于点P , 连接AP并延长交BC于点D , 则下列说法:
MN的长为半径画弧,两弧交于点P , 连接AP并延长交BC于点D , 则下列说法: 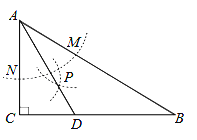
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】若数轴上点A表示的数是1,则与点A距离为2的点所表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角板ABC中,∠A=30°,BC=1.将其绕直角顶点C逆时针旋转一个角
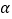 (
(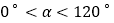 且
且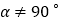 ),得到Rt△
),得到Rt△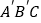 .
.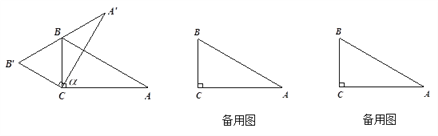
(1)如图,当边
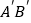 经过点B时,求旋转角
经过点B时,求旋转角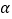 的度数;
的度数;(2)在三角板旋转的过程中,边
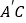 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥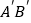 交
交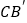 边于点E,联结BE.
边于点E,联结BE.①当
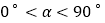 时,设AD=
时,设AD=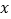 ,BE=
,BE=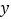 ,求
,求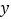 与
与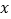 之间的函数解析式及自变量
之间的函数解析式及自变量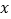 的取值范围;
的取值范围;②当
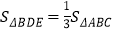 时,求AD的长.
时,求AD的长.
相关试题

