【题目】如图,二次函数y= ![]() +bx﹣
+bx﹣ ![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.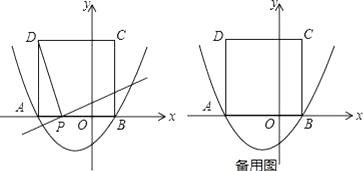
(1)b=;点D的坐标:;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
参考答案:
【答案】
(1)1,(﹣3,4)
(2)解:直线PE交y轴于点E,如图1,
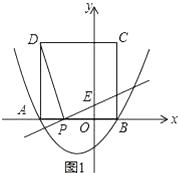
假设存在点P,使得OE的长为1,设OP=a,则AP=3﹣a,
∵DP⊥AE,∠APD+∠DPE+∠EPO=180°,
∴∠EPO=90°﹣∠APD=∠ADP,
tan∠ADP= ![]() =
= ![]() ,tan∠EPO=
,tan∠EPO= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() ﹣3a+4=0,
﹣3a+4=0,
△= ![]() ﹣4×4=﹣7<0,无解,
﹣4×4=﹣7<0,无解,
故线段AO上不存在点P(点P不与A、O重合),使得OE的长为1.
(3)解:假设存在这样的点P,DE交x轴于点M,如图2,
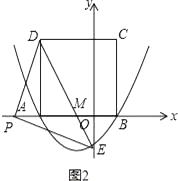
∵△PED是等腰三角形,
∴DP=PE,
∵DP⊥PE,四边形ABCD为正方形
∴∠EPO+∠APD=90°,∠DAP=90°,∠PAD+∠APD=90°,
∴∠EPO=∠PDA,∠PEO=∠DPA,
在△PEO和△DAP中,
∠EPO=∠PDA,DP=PE,∠PEO=∠DPA,
∴△PEO≌△DAP,
∴PO=DA=4,OE=AP=PO﹣AO=4﹣3=1,
∴点P坐标为(﹣4,0).
∵DA⊥x轴,
∴DA∥EO,
∴∠ADM=∠OEM(两直线平行,内错角相等),
又∵∠AMD=∠OME(对顶角),
∴△DAM∽EOM,
∴ ![]() ,
,
∵OM+MA=OA=3,
∴MA= ![]() ×3=
×3= ![]() ,
,
△PED与正方形ABCD重叠部分△ADM面积为 ![]() ×AD×AM=
×AD×AM= ![]() ×4×
×4× ![]() =
= ![]() .
.
答:存在这样的点P,点P的坐标为(﹣4,1),此时△PED与正方形ABCD重叠部分的面积为 ![]() .
.
【解析】(1)∵点A(﹣3,0)在二次函数y= ![]() +bx﹣
+bx﹣ ![]() 的图象上,
的图象上,
∴0= ![]() ﹣3b﹣
﹣3b﹣ ![]() ,解得b=1,
,解得b=1,
∴二次函数解析式为y= ![]() +x﹣
+x﹣ ![]() =
= ![]() (x+3)(x﹣1),
(x+3)(x﹣1),
∴点B(1,0),AB=1﹣(﹣3)=4,
∵四边形ABCD为正方形,
∴AD=AB=4,
∴点D(﹣3,4),
所以答案是:1;(﹣3,4).
【考点精析】掌握正方形的性质和相似三角形的判定与性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,图中
 和
和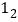 分别表示他们各自到A地的距离
分别表示他们各自到A地的距离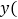 千米
千米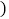 与时间
与时间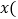 小时
小时 的关系,根据图中提供的信息,解答下列问题:
的关系,根据图中提供的信息,解答下列问题: 图中哪条线表示甲到A地的距离与时间的关系?
图中哪条线表示甲到A地的距离与时间的关系? 甲,乙两人的速度分别是多少?
甲,乙两人的速度分别是多少? 求P点的坐标,并解释P点的实际意义.
求P点的坐标,并解释P点的实际意义.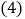 甲出发多长时间后,两人相距30千米?
甲出发多长时间后,两人相距30千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(一)问题提出:如何把n个边长为1的正方形,剪拼成一个大正方形?
(二)解决方法
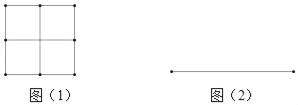
探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.
问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(1)计算:拼成的大正方形的面积为5,边长为
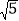 ,可表示成
,可表示成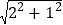 ;
;(2)剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
(3)拼图:以图(3)中的虚线为边,拼成一个边长为
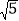 的大正方形,如图(4).
的大正方形,如图(4).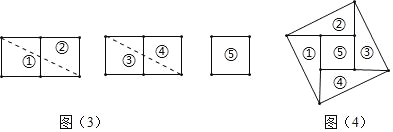
问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
(1)计算:拼成的大正方形的面积为____,边长为_____,可表示成____;
(2)剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
(3)拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击队有甲、乙两名射手,他们各自射击7次,射中靶的环数记录如下:
甲:8,8,8,9,6,8,9
乙:10,7,8,8,5,10,8
(1)分别求出甲、乙两名射手打靶环数的平均数、众数、中位数;
(2)如果要选择一名成绩比较稳定的射手,代表射击队参加比赛,应如何选择?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在平面直角坐标系中.
(1)写出△ABC各顶点的坐标.
(2)把△ABC向上平移2个单位,再向右平移2个单位得△A'B'C',在图中画出△A'B'C',并写出A'、B'、C'的坐标.
(3)求出
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C、D在⊙O上,∠BAC=50°,则∠ADC为( )
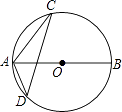
A.40°
B.50°
C.80°
D.100° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
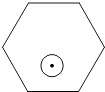
A.πr2
B.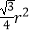
C.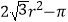 r2
r2
D.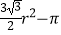 r2
r2
相关试题

