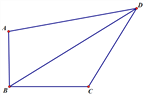
【题目】如图,在四边形ABCD 中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10![]() ,
,
(1)求四边形ABCD的面积(2)求 BD的长
参考答案:
【答案】(1)74;(2)2![]()
【解析】(1)根据勾股定理的逆定理得出△ABC是直角三角形,进而求出四边形面积即可;
(2)过点D作DE⊥BC,交BC的延长线与点E,利用△ABC∽△CED求出BD的长即可.
(1)连接AC,
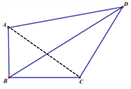
∵∠ABC=90°,
∴△ABC为直角三角形,AB=8,BC=6,∴AC=10,
又∵DA=10![]() ,CD=10,
,CD=10,
∴102+102=(10![]() )2
)2
AC2+CD2=DA2
所以△ACD为直角三角形.
四边形ABCD的面积S△ABC+S△ACD=![]() =74;
=74;
(2) 过点D作DE⊥BC,交BC的延长线与点E
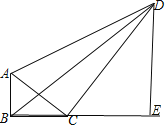
∵∠DEC=90°,∴∠DCE+∠CDE=90°,
所以∠DCE+∠ACB=90°,
∴∠CDE=∠ACB,又∵∠ABC=90°,
∴△ABC∽△CED
∴![]()
∴CE=6,DE=8.
∴BE=BC+CE=14,
在Rt△DEB中,
DB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+3和2x-1成正比例,且x=2时,y=1。
(1)写出y与x的函数解析式。
(2)当0≤x≤3 时,y的最大值和最小值分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
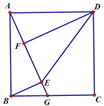
(1)求证:△ABE≌△DAF;
(2)若BE=8,EF=7,求CD的长.
-
科目: 来源: 题型:
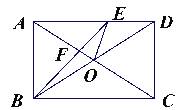
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在已知,口ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证: 四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, 点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,tanC=
 ,AC=3
,AC=3 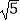 ,AB=4,求△ABC的周长.
,AB=4,求△ABC的周长. 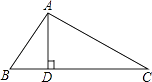
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某班学生的一次数学成绩进行统计,各分数段的人数如图所示,根据图示信息填空:
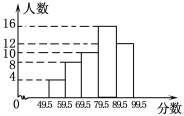
(1)该班有学生________人;
(2)成绩在69.5~79.5之间的人数为________人;
(3)79.5分以上的为优秀,该班的优秀率是________.
相关试题

