【题目】如图,在△ABC中,AD是BC边上的高,tanC= ![]() ,AC=3
,AC=3 ![]() ,AB=4,求△ABC的周长.
,AB=4,求△ABC的周长. 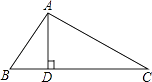
参考答案:
【答案】解:在Rt△ADC中,tanC= ![]() =
= ![]() , 设AD=k,CD=2k,
, 设AD=k,CD=2k,
AC= ![]() =
= ![]() k,
k,
∵AC=3 ![]() ,
,
∴ ![]() k=3
k=3 ![]() ,解得k=3,
,解得k=3,
∴AD=3,CD=6,
在Rt△ABD中,
BD= ![]() =
= ![]() =
= ![]() ,
,
∴△ABC的周长=AB+AC+BD+CD=4+3 ![]() +
+ ![]() +6=10+3
+6=10+3 ![]() +
+ ![]()
【解析】在Rt△ADC中,根据正切的定义得到tanC= ![]() =
= ![]() ,则可设AD=k,CD=2k,接着利用勾股定理得到AC=
,则可设AD=k,CD=2k,接着利用勾股定理得到AC= ![]() k,则
k,则 ![]() k=3
k=3 ![]() ,解得k=3,所以AD=3,CD=6,然后在Rt△ABD中,利用勾股定理计算出BD=
,解得k=3,所以AD=3,CD=6,然后在Rt△ABD中,利用勾股定理计算出BD= ![]() ,再根据三角形的周长的定义求解.
,再根据三角形的周长的定义求解.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
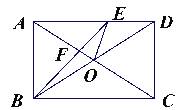
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD 中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10
 ,
,(1)求四边形ABCD的面积(2)求 BD的长
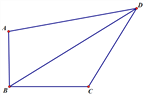
-
科目: 来源: 题型:
查看答案和解析>>【题目】在已知,口ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证: 四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, 点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.



-
科目: 来源: 题型:
查看答案和解析>>【题目】对某班学生的一次数学成绩进行统计,各分数段的人数如图所示,根据图示信息填空:
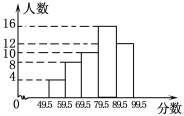
(1)该班有学生________人;
(2)成绩在69.5~79.5之间的人数为________人;
(3)79.5分以上的为优秀,该班的优秀率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
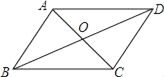
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
相关试题

