【题目】在已知,口ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证: 四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, 点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为秒,若当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.



参考答案:
【答案】(1)见解析;(2)5cm;(3) ![]() 秒.
秒.
【解析】(1)根据全等推出OE=OF,得出平行四边形AFCE,根据菱形判定推出即可;
(2)根据菱形性质得出AF=CF,根据勾股定理得出方程,求出方程的解即可;
(3)分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为平行四边形
∵AC⊥EF
∴四边形![]() 为菱形
为菱形
(2)∵EF垂直平分AC
∴AF=CF
∴设AF=CF=xcm,则BF=(8﹣x)cm,
在Rt△ABF中,AB=4cm,由勾股定理得![]() ,
,
解得x=5,∴AF=5cm;
(3)∵ 显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形,
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒1cm,点Q的速度为每秒0.8cm,运动时间为t秒,
∴PC=t,QA=12﹣0.8t,∴t=12﹣0.8t,解得![]() ,
,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时![]() 秒
秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
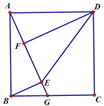
(1)求证:△ABE≌△DAF;
(2)若BE=8,EF=7,求CD的长.
-
科目: 来源: 题型:
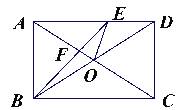
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
-
科目: 来源: 题型:
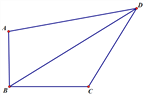
查看答案和解析>>【题目】如图,在四边形ABCD 中,∠ABC=90°,AB=6,BC=8,CD=10,AD=10
 ,
,(1)求四边形ABCD的面积(2)求 BD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,tanC=
 ,AC=3
,AC=3 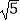 ,AB=4,求△ABC的周长.
,AB=4,求△ABC的周长. 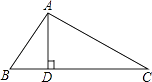
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某班学生的一次数学成绩进行统计,各分数段的人数如图所示,根据图示信息填空:
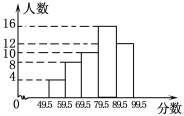
(1)该班有学生________人;
(2)成绩在69.5~79.5之间的人数为________人;
(3)79.5分以上的为优秀,该班的优秀率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

相关试题

