【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:![]() .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
参考答案:
【答案】(1)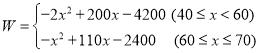 ;(2)该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元;(3)45≤x≤55.
;(2)该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元;(3)45≤x≤55.
【解析】
试题分析:(1)根据:年利润=(售价﹣成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案;
(3)根据题意知W≥750,可列关于x的不等式,求解可得x的范围.
试题解析:(1)当40≤x<60时,W=(x﹣30)(﹣2x+140)=![]() ,当60≤x≤70时,W=(x﹣30)(﹣x+80)=
,当60≤x≤70时,W=(x﹣30)(﹣x+80)=![]() ;
;
综上所述: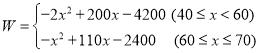 ;
;
(2)当40≤x<60时,W=![]() =
=![]() ,∴当x=50时,W取得最大值,最大值为800万元;
,∴当x=50时,W取得最大值,最大值为800万元;
当60≤x≤70时,W=![]() =
=![]() ,∴当x>55时,W随x的增大而减小,∴当x=60时,W取得最大值,最大值为:
,∴当x>55时,W随x的增大而减小,∴当x=60时,W取得最大值,最大值为:![]() =600,∵800>600,∴当x=50时,W取得最大值800,答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元;
=600,∵800>600,∴当x=50时,W取得最大值800,答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元;
(3)当40≤x<60时,由W≥750得:![]() ≥750,解得:45≤x≤55,当60≤x≤70时,W的最大值为600<750,∴要使企业销售该产品的年利润不少于750万元,该产品的售价x(元/件)的取值范围为45≤x≤55.
≥750,解得:45≤x≤55,当60≤x≤70时,W的最大值为600<750,∴要使企业销售该产品的年利润不少于750万元,该产品的售价x(元/件)的取值范围为45≤x≤55.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示:3,﹣3,﹣1
 ,0,4.5,并用“<”按从小到大的顺序连接.
,0,4.5,并用“<”按从小到大的顺序连接. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)(﹣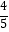 )×13+(﹣
)×13+(﹣ 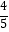 )×2﹣(﹣
)×2﹣(﹣ 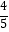 )×5
)×5
(3)﹣22+5×(﹣3)﹣(﹣4)÷4
(4)﹣14﹣(1﹣0.5)× ×[2﹣(﹣3)2].
×[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
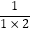 =1﹣
=1﹣  ,
, 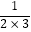 =
=  ﹣
﹣  ,
, 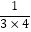 =
=  ﹣
﹣  ,
,
把以上三个等式两边分别相加得: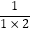 +
+ 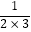 +
+ 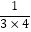 =1﹣
=1﹣  +
+  ﹣
﹣  +
+  ﹣
﹣  =1﹣
=1﹣  =
=  .
.
(1)猜想并写出: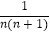 = .
= .
(2)直接写出下列式子的计算结果: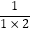 +
+ 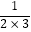 +
+ 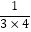 +…+
+…+ 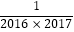 = .
= .
(3)探究并计算: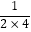 +
+ 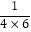 +
+ 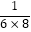 +…+
+…+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列说法中是错误的是( )
A.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
B.在△ABC中,∠C=∠A﹣∠B,则△ABC为直角三角形
C.在△ABC中,若a=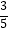 c,b=
c,b= 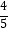 c,则△ABC为直角三角形
c,则△ABC为直角三角形
D.在△ABC中,若a:b:c=2:2:4,则△ABC为直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】平方根和立方根都是本身的数是( )
A. 0 B. 0和1 C. ±1 D. 0和±1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2m+1,m+9)在第一象限,且点A到x轴和y轴的距离相等,求点A的坐标.
相关试题

