【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
参考答案:
【答案】(1) ①两;②8;③4;④48.(2)①23; ②67
【解析】分析:(1)①根据110592大于1000而小于1000000,即可确定110592的立方根是2位数;
②根据一个数的立方的个位数就是这个数的个位数的立方的个位数,据此即可确定;
③根据数的立方的计算方法即可确定;
④根据前面判断即可得出结论.
(2)首先根据一个数的立方的个位数就是这个数的个位数的立方的个位数确定个位数,然后一次确定十位数.
详解:(1)①103=1000,1003=1000000,你能确定110592的立方根是2位数.
故答案为:两;
②由110592的个位数是2,你能确定110592的立方根的个位数是 8.
故答案为:8.
③如果划去110592后面的三位592得到数110,而43=64,53=125,由此你能确定110592的立方根的十位数是4.
④因此110592的立方根是 48.
(2)①![]() 23;
23;
②![]() 67.
67.
-
科目: 来源: 题型:
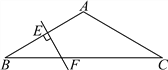
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F.若BF=3cm.求BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于P(x,y)作变换得到P′(﹣y+1,x+1),例如:A1(3,1)作上述变换得到A2(0,4),再将A2做上述变换得到A3___________,这样依次得到A1,A2,A3,…An;…,则A2018的坐标为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点
 .
.(1)点M到y轴的距离为1时,M的坐标?
(2)点
 且MN//x轴时,M的坐标?
且MN//x轴时,M的坐标? -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:
如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.

小明的思路是:
过点P作PE//AB,

∴∠PAB+∠APE=180°.
∵∠PAB=130°,∴∠APE=50°
∵AB//CD,PE//AB,∴PE//CD,
∴∠PCD+∠CPE=180°.
∵∠PCD=120°,∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
如果AB与CD平行关系不变,动点P在直线AB、CD所夹区域内部运动时,∠PAB,∠PCD的度数会跟着发生变化.
(1)如图3,当动点P运动到直线AC右侧时,请写出∠PAB,∠PCD和∠APC之间的数量关系?并说明理由.

(2)如图4,AQ,CQ分别平分∠PAB,∠PCD,那么∠AQC和角∠APC有怎择的数量关系?

(3)如图5,点P在直线AC的左侧时,AQ,CQ仍然平分∠PAB,∠PCD,请直接写出∠AQC和角∠APC的数量关系 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.

(1)求证:BE=DF;
(2)若 M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由). -
科目: 来源: 题型:
查看答案和解析>>【题目】某校某年级秋游,若租用48座客车若干辆,则正好坐满;若租用64座客车,则能少租1辆,且有一辆车没有坐满,但超过一半.
(1)需租用48座客车多少辆? 解:设需租用48座客车x辆.则需租用64座客车辆.当租用64座客车时,未坐满的那辆车还有个空位(用含x的代数式表示).由题意,可得不等式组:解这个不等式组,得: .
因此,需租用48座客车辆.
(2)若租用48座客车每辆250元,租用64座客车每辆300元,应租用哪种客车较合算?
相关试题

