[题目]在平面直角坐标系中.对于P(x.y)作变换得到P′(﹣y+1.x+1).例如:A1(3.1)作上述变换得到A2(0.4).再将A2做上述变换得到A3 .这样依次得到A1.A2.A3.-An,-.则A2018的坐标为．题目和参考答案 ——青夏教育精英家教网—

【题目】在平面直角坐标系中，对于P(x，y)作变换得到P′(﹣y+1，x+1)，例如：A1(3，1)作上述变换得到A2(0，4)，再将A2做上述变换得到A3___________，这样依次得到A1，A2，A3，…An；…，则A2018的坐标为___________．

参考答案：

【答案】(﹣3，1) (0，4)

【解析】

按照变换规则可以推出各点坐标每4次一个循环，则2018在一个循环的第二次变换．

解：按照变换规则，A3坐标为（﹣3，1），A4坐标（0，﹣2），A5坐标（3，1）则可知，每4次一个循环，

∵2018＝504×4+2，

∴A2018坐标为（0，4），

故答案为：（﹣3，1），（0，4）

相关试题

科目： 来源： 题型：

【题目】如图，直线AB、CD相交于点O，OE把分成两部分；
（1）直接写出图中的对顶角为，的邻补角为；
（2）若，且，求的度数.
查看答案和解析>>
科目： 来源： 题型：

【题目】将命题“钝角大于它的补角”写成“如果…那么”的形式：___________．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC中，AB＝AC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F.若BF＝3cm.求BC.
查看答案和解析>>
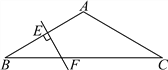
科目： 来源： 题型：

【题目】已知平面直角坐标系中有一点.
（1）点M到y轴的距离为1时，M的坐标？
（2）点且MN//x轴时，M的坐标？
查看答案和解析>>
科目： 来源： 题型：

【题目】数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：
①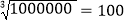，，又，
，
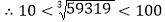能确定59319的立方根是个两位数．
②59319的个位数是9，又，
能确定59319的立方根的个位数是9．
③如果划去59319后面的三位319得到数59，
而，则，可得，
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
（1）现在换一个数110592，按这种方法求立方根，请完成下列填空.
①它的立方根是位数．
②它的立方根的个位数是．
③它的立方根的十位数是．
④110592的立方根是．
（2）请直接填写结果：
① ；
② ；
查看答案和解析>>
科目： 来源： 题型：

【题目】问题情景：
如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
小明的思路是：
过点P作PE//AB，
∴∠PAB+∠APE=180°．
∵∠PAB=130°，∴∠APE=50°
∵AB//CD，PE//AB，∴PE//CD，
∴∠PCD+∠CPE=180°．
∵∠PCD=120°，∴∠CPE=60°
∴∠APC=∠APE+∠CPE=110°．
问题迁移：
如果AB与CD平行关系不变，动点P在直线AB、CD所夹区域内部运动时，∠PAB，∠PCD的度数会跟着发生变化．
（1）如图3，当动点P运动到直线AC右侧时，请写出∠PAB，∠PCD和∠APC之间的数量关系？并说明理由．
（2）如图4，AQ，CQ分别平分∠PAB，∠PCD，那么∠AQC和角∠APC有怎择的数量关系？
（3）如图5，点P在直线AC的左侧时，AQ，CQ仍然平分∠PAB，∠PCD，请直接写出∠AQC和角∠APC的数量关系．
查看答案和解析>>