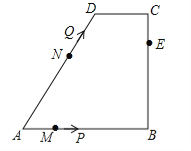
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.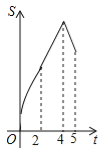 B.
B.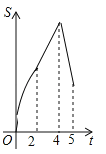 C.
C.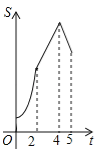 D.
D.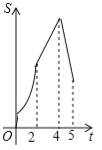
参考答案:
【答案】D.
【解析】∵AD=5,AN=3,∴DN=2,如图1,过点D作DF⊥AB,∴DF=BC=4,在RT△ADF中,AD=5,DF=4,根据勾股定理得,AF=![]() =3,∴BF=CD=2,当点Q到点D时用了2s,∴点P也运动2s,∴AP=3,即QP⊥AB,∴只分三种情况:
=3,∴BF=CD=2,当点Q到点D时用了2s,∴点P也运动2s,∴AP=3,即QP⊥AB,∴只分三种情况:
①当0<t≤2时,如图1,过Q作QG⊥AB,过点D作DF⊥AB,QG∥DF,∴![]() ,由题意得,NQ=t,MP=t,∵AM=1,AN=3,∴AQ=t+3,∴
,由题意得,NQ=t,MP=t,∵AM=1,AN=3,∴AQ=t+3,∴![]() ,∴QG=
,∴QG=![]() (t+3),∵AP=t+1,∴S=S△APQ=
(t+3),∵AP=t+1,∴S=S△APQ=![]() AP×QG=
AP×QG=![]() ×(t+1)×
×(t+1)×![]() (t+3)=
(t+3)=![]() ,当t=2时,S=6;
,当t=2时,S=6;
②当2<t≤4时,如图2,∵AP=AM+t=1+t,∴S=S△APQ=![]() AP×BC=
AP×BC=![]() (1+t)×4=2(t+1)=2t+2,当t=4时,S=8;
(1+t)×4=2(t+1)=2t+2,当t=4时,S=8;
③当4<t≤5时,如图3,由题意得CQ=t﹣4,PB=t+AM﹣AB=t+1﹣5=t﹣4,∴PQ=BC﹣CQ﹣PB=4﹣(t﹣4)﹣(t﹣4)=12﹣2t,∴S=S△APQ=![]() PQ×AB=
PQ×AB=![]() ×(12﹣2t)×5=﹣5t+50,当t=5时,S=5;
×(12﹣2t)×5=﹣5t+50,当t=5时,S=5;
∴S与t的函数关系式分别是①S=S△APQ=![]() ,当t=2时,S=6,②S=S△APQ=2t+2,当t=4时,S=8,③∴S=S△APQ=﹣5t+50,当t=5时,S=5,综合以上三种情况,D正确.故选D.
,当t=2时,S=6,②S=S△APQ=2t+2,当t=4时,S=8,③∴S=S△APQ=﹣5t+50,当t=5时,S=5,综合以上三种情况,D正确.故选D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,
 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.

(1)求证:AD=CE;
(2)求证:AD和CE垂直. -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当方法解方程:(1)x2﹣4=3x;(2)(2x+3)2=9(x﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】向东走-8米的意义是( )
A.向东走8米
B.向西走8米
C.向西走-8米
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】应用方程组解决实际问题的步骤:理解问题;____________;____________;____________.
相关试题

