【题目】如图,抛物线![]() 与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)P点坐标为(
;(2)P点坐标为(![]() ,
,![]() )时,四边形ABPC的面积最大,最大面积为
)时,四边形ABPC的面积最大,最大面积为![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)把B、C两点坐标代入抛物线解析式可得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H.

在![]() 中,令y=0可得
中,令y=0可得![]() ,解得x=﹣1或x=3,∴A点坐标为(﹣1,0),∴AB=3﹣(﹣1)=4,且OC=3,∴S△ABC=
,解得x=﹣1或x=3,∴A点坐标为(﹣1,0),∴AB=3﹣(﹣1)=4,且OC=3,∴S△ABC=![]() ABOC=
ABOC=![]() ×4×3=6,∵B(3,0),C(0,﹣3),∴直线BC解析式为y=x﹣3,设P点坐标为(x,
×4×3=6,∵B(3,0),C(0,﹣3),∴直线BC解析式为y=x﹣3,设P点坐标为(x,![]() ),则M点坐标为(x,x﹣3),∵P点在第四限,∴PM=
),则M点坐标为(x,x﹣3),∵P点在第四限,∴PM=![]() =
=![]() ,∴S△PBC=
,∴S△PBC=![]() PMOH+
PMOH+![]() PMHB=
PMHB=![]() PM(OH+HB)=
PM(OH+HB)=![]() PMOB=
PMOB=![]() PM,∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,∵PM=
PM,∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,∵PM=![]() =
=![]() ,∴当x=
,∴当x=![]() 时,PMmax=
时,PMmax=![]() ,则S△PBC=
,则S△PBC=![]() =
=![]() ,此时P点坐标为(
,此时P点坐标为(![]() ,
,![]() ),S四边形ABPC=S△ABC+S△PBC=6+
),S四边形ABPC=S△ABC+S△PBC=6+![]() =
=![]() ,即当P点坐标为(
,即当P点坐标为(![]() ,
,![]() )时,四边形ABPC的面积最大,最大面积为
)时,四边形ABPC的面积最大,最大面积为![]() ;
;
(3)如图2,设直线m交y轴于点N,交直线l于点G,则∠AGP=∠GNC+∠GCN,当△AGB和△NGC相似时,必有∠AGB=∠CGB,又∠AGB+∠CGB=180°,∴∠AGB=∠CGB=90°,∴∠ACO=∠OBN,在Rt△AON和Rt△NOB中,∵∠AOC=∠NOB,OC=OB,∠ACO=∠NBO,∴Rt△AON≌Rt△NOB(ASA),∴ON=OA=1,∴N点坐标为(0,﹣1),设直线m解析式为y=kx+d,把B、N两点坐标代入可得![]() ,解得:
,解得: ,∴直线m解析式为
,∴直线m解析式为![]() ,即存在满足条件的直线m,其解析式为
,即存在满足条件的直线m,其解析式为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )

A.35°
B.45°
C.55°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组的基本思想是_________,也就是把二元一次方程组转化为______________. 消元的方法有:_____________、_______________等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题;
例题,已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴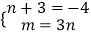
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式3x2+5x﹣m有一个因式是(3x﹣1),求另一个因式以及m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,
 ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.

(1)求证:AD=CE;
(2)求证:AD和CE垂直. -
科目: 来源: 题型:
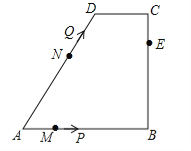
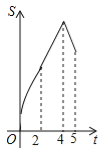
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.
 B.
B.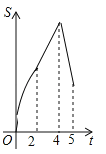 C.
C.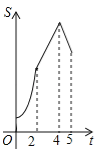 D.
D.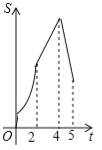
相关试题

