【题目】如图,在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 分别在
分别在![]() 轴的正半轴和x轴的正半轴上,
轴的正半轴和x轴的正半轴上,![]() 的面积为
的面积为![]() ,过点
,过点![]() 作直线
作直线![]() 轴.
轴.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是第一象限直线
是第一象限直线![]() 上一动点,连接
上一动点,连接![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 轴于点D,设点
轴于点D,设点![]() 的纵坐标为
的纵坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,过点![]() 作直线
作直线![]() ,交
,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 与
与![]() 的关系式:
的关系式:![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)由OA=OB,根据面积求出OA的长即可得A点坐标;(2)分0<d<6,d>6,d=6三种情况,当0<d<6时,过C作CH⊥x轴,根据锐角互余的关系可得∠CBH=∠BDO,利用AAS可证明△CBH≌△BDO,进而可得OD=BH,根据OH=AC=d,OH+HB=OB可得d-t=6,同理可得d>6,d=6时,d-t=6;(3)当0<d<6时,由OA=OB,∠AOB=90°,可得∠OAB=∠OBA=45°,在![]() 中,
中,![]() ,可得AE=AD,根据OD=BH,AC=OH,CE=AE+AC可求出CE的长,进而可得OF的长,根据OF=OD可求出t的值,根据(2)所得关系式可求出AC的长进而可得AE的长,即可求出E点坐标,同理可求出d>6时E点坐标,当d=6时,E点不存在.
,可得AE=AD,根据OD=BH,AC=OH,CE=AE+AC可求出CE的长,进而可得OF的长,根据OF=OD可求出t的值,根据(2)所得关系式可求出AC的长进而可得AE的长,即可求出E点坐标,同理可求出d>6时E点坐标,当d=6时,E点不存在.
(1)如图![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
∵OA=OB,
∴OA2=36,
∴OA=6
∴点![]() 的坐标为
的坐标为![]()
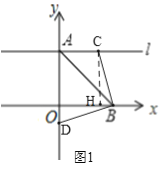
(2)①当0<d<6时,如图1,此时t<0,
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴∠CBH=∠BDO,
∵∠CHB=∠BOD=90°,
∴△CBH≌△BDO,
∴OD=BH,
∵OH=AC=d,OH+HB=OB,
∴d-t=6.
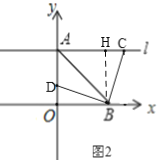
同理,当![]() 时,如图2,可得CH=OD,
时,如图2,可得CH=OD,
∴AC=AH+CH=6+OD,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴d-t=6,
![]() 当
当![]() 时,
时,![]()
∴![]() 与
与![]() 的关系式为d-t=6.
的关系式为d-t=6.
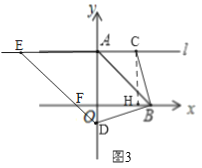
(3)当![]() 时,如图
时,如图![]()
![]()
∴∠ABO=∠BAO=45°,
∵DE//AB,
∴∠EDA=∠BOA=45°,
在![]() 中,
中,![]() ,
,
∴AE=AD,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴t=-2,
∴d-(-2)=6,
∴d=4,即AC=4,
∴EA=CE-AC=12-4=8,
∴点![]() 的坐标为
的坐标为![]()
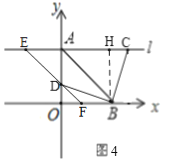
同理,当![]() 时,如图
时,如图![]() ,可得CE=12.OD=OF=
,可得CE=12.OD=OF=![]() =2,
=2,
∴t=2,
∴d-2=6,
∴d=8,即AC=8,
∴AE=12-8=4,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,点
时,点![]() 不存在,
不存在,
综上,点![]() 的坐标为
的坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且
 .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,线段AB的两个端点是A(﹣5,1),B(﹣2,3),平移线段AB得到线段A1B1 , 若点A的对应点A1的坐标为(1,2),则点B的对应点B1的坐标为 .
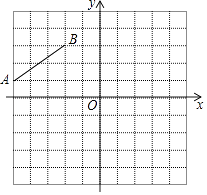
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。
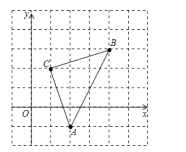
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
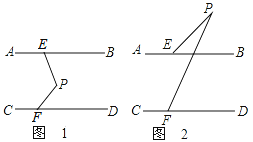
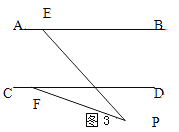
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A.
 B.
B.  C.
C.  D. 1
D. 1
相关试题

