【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

参考答案:
【答案】对顶角相等,CE,BD,内错角相等,两直线平行,两直线平行,同位角相等
【解析】
此题主要利用对顶角相等,得出∠2=∠3,∠1=∠4,然后等量代换得出∠3=∠4;根据内错角相等,两直线平行,得出BD∥CE,再根据平行线的性质:两直线平行,同位角相等,得出∠C=∠ABD,然后证出∠D=∠ABD,进而证得DF∥AC.
∵∠1=∠2,( 已知 )
又∵∠2=∠3 ,∠1=∠4( 对顶角相等 )
∴∠3=∠4( 等量代换 )
∴_____BD___∥__CE_____( 内错角相等,两直线平行 )
∴∠C=∠ABD( 两直线平行,同位角相等 )
∵∠C=∠D(已知 )
∴∠D=∠ABD(等量代换 )
∴DF∥AC( 内错角相等,两直线平行 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD与EF相交.
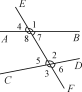
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
-
科目: 来源: 题型:
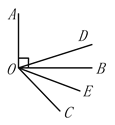
查看答案和解析>>【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知抛物线y=ax2+bx﹣3的对称轴为x=1,与x轴分别交于A、B两点,与y轴交于点C,一次函数y=x+1经过A,且与y轴交于点D.
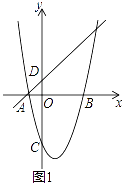
(1)求该抛物线的解析式.
(2)如图(2),点P为抛物线B、C两点间部分上的任意一点(不含B,C两点),设点P的横坐标为t,设四边形DCPB的面积为S,求出S与t的函数关系式,并确定t为何值时,S取最大值?最大值是多少?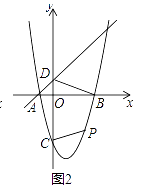
(3)如图(3),将△ODB沿直线y=x+1平移得到△O′D′B′,设O′B′与抛物线交于点E,连接ED′,若ED′恰好将△O′D′B′的面积分为1:2两部分,请直接写出此时平移的距离.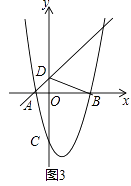
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( )
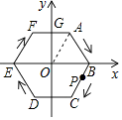
A.(1,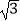 )
)
B.(﹣1,﹣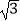 )
)
C.(1,﹣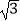 )
)
D.(﹣1,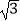 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为
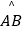 的中点,D为OB的中点,则图中阴影部分的面积为cm2 .
的中点,D为OB的中点,则图中阴影部分的面积为cm2 . 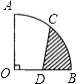
-
科目: 来源: 题型:
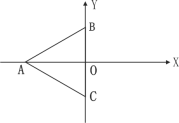
查看答案和解析>>【题目】如图,等边三角形ABC的顶点B(0,2),A在x轴负半轴上、C在y轴负半轴上.
(1)写出A、C两点的坐标;
(2)求△ABC的面积和周长.
相关试题

