【题目】如图,在平面直角坐标系中,线段AB的两个端点是A(﹣5,1),B(﹣2,3),平移线段AB得到线段A1B1 , 若点A的对应点A1的坐标为(1,2),则点B的对应点B1的坐标为 . 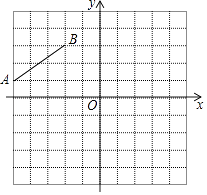
参考答案:
【答案】(4,4)
【解析】解:∵A(﹣5,1)平移后对应点A1的坐标为(1,2),
∴点A向右平移6个单位,向上平移1个单位,
∴点B也向右平移6个单位,向上平移1个单位,
∵B(﹣2,3),
∴点B的对应点B1的坐标为(﹣2+6,3+1),
即(4,4),
所以答案是:(4,4).
【考点精析】关于本题考查的坐标与图形变化-平移,需要了解新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )

A.②④
B.①④
C.①③
D.②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是长方形, ∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=4,AD=BC=6,点A的坐标为(3,2).动点P的运动速度为每秒a个单位长度,动点Q的运动速度为每秒b个单位长度,且
 .设运动时间为t,动点P、Q相遇则停止运动.
.设运动时间为t,动点P、Q相遇则停止运动.(1) 求a,b的值;
(2) 动点P,Q同时从点A出发,点P沿长方形ABCD的边界逆时针方向运动,点Q沿长方形ABCD的边界顺时针方向运动,当t为何值时P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
(3) 动点P从点A出发,同时动点Q从点D出发:
①若点P、Q均沿长方形ABCD的边界顺时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标;
②若点P、Q均沿长方形ABCD的边界逆时针方向运动,t为何值时,P、Q两点相遇?求出相遇时P、Q所在位置的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 是坐标原点,点
是坐标原点,点 分别在
分别在 轴的正半轴和x轴的正半轴上,
轴的正半轴和x轴的正半轴上,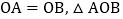 的面积为
的面积为 ,过点
,过点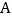 作直线
作直线 轴.
轴.(1)求点
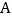 的坐标;
的坐标;(2)点
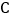 是第一象限直线
是第一象限直线 上一动点,连接
上一动点,连接 .过点
.过点 作
作 ,交
,交 轴于点D,设点
轴于点D,设点 的纵坐标为
的纵坐标为 ,点
,点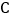 的横坐标为
的横坐标为 ,求
,求 与
与 的关系式;
的关系式;(3)在(2)的条件下,过点
 作直线
作直线 ,交
,交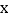 轴于点
轴于点 ,交直线
,交直线 于点
于点 ,当
,当 时,求点
时,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
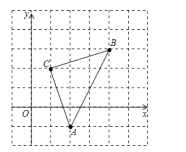
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
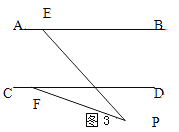
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
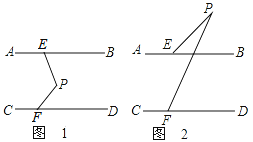
相关试题

