【题目】如图,直线AB∥CD,点P在两平行直线之间,点E在AB上,点F在CD上,连接PE、PF。
(1)∠PEB、∠PFD、∠EPF满足什么数量关系?请说明理由。
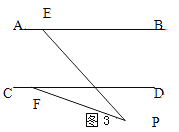
(2)如果点P在两平行线外时,试探究∠PEB、∠PFD、∠EPF之间的数量关系。(不需说明理由)
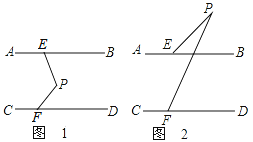
参考答案:
【答案】(1) ∠EPF=∠PEB+∠PFD; (2) ∠PFD=∠PEB+∠EPF;∠PEB=∠PFD+∠EPF.
【解析】
(1)过点P作PH∥AB∥CD,根据平行线的性质:两直线平行,内错角相等即可证得;(2)若点P在直线AB上方时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得;若点P在直线AB下方时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得.
解:(1)∠PEB,∠PFD,∠P满足的数量关系是∠EPF=∠PEB+∠PFD;
理由如下:如图1,过点P作PH∥AB∥CD
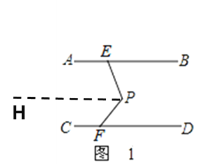
∴∠PEB=∠EPH,∠PFD=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠PEB+∠PFD;
(2)如图2,若点P在直线AB上方时,
∠PEB,∠PFD,∠P满足的数量关系是∠PFD=∠PFB+∠EPF;
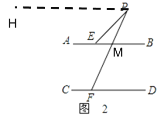
理由:过点P作PH∥AB∥CD
∴∠FPH=∠PFD=∠PMB
而∠PMB=∠PFB+∠EPF∴∠PFD=∠PFB+∠EPF;
如图3,若点P在直线AB下方时,
∠PEB,∠PFD,∠P满足的数量关系是∠PEB=∠PFD+∠EPF;
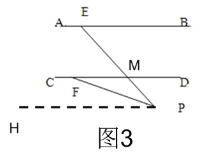
理由: 过点P作PH∥AB∥CD
∴∠PEB=∠EPH=∠DMP,而∠DMP=∠PFD+∠EPF.
∴∠PEB=∠PFD+∠EPF;
-
科目: 来源: 题型:
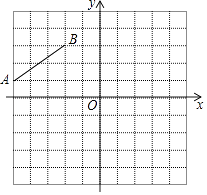
查看答案和解析>>【题目】如图,在平面直角坐标系中,线段AB的两个端点是A(﹣5,1),B(﹣2,3),平移线段AB得到线段A1B1 , 若点A的对应点A1的坐标为(1,2),则点B的对应点B1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 是坐标原点,点
是坐标原点,点 分别在
分别在 轴的正半轴和x轴的正半轴上,
轴的正半轴和x轴的正半轴上,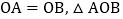 的面积为
的面积为 ,过点
,过点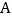 作直线
作直线 轴.
轴.(1)求点
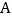 的坐标;
的坐标;(2)点
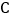 是第一象限直线
是第一象限直线 上一动点,连接
上一动点,连接 .过点
.过点 作
作 ,交
,交 轴于点D,设点
轴于点D,设点 的纵坐标为
的纵坐标为 ,点
,点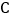 的横坐标为
的横坐标为 ,求
,求 与
与 的关系式;
的关系式;(3)在(2)的条件下,过点
 作直线
作直线 ,交
,交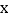 轴于点
轴于点 ,交直线
,交直线 于点
于点 ,当
,当 时,求点
时,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
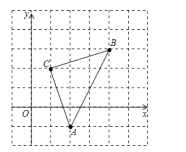
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
(1)写出点A、B的坐标:A(_____,_____)、B(_____,_____);
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,写出A′、B′、C′三点坐标;
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解不等式组: .
.
(2)化简:(x﹣ )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

相关试题

