【题目】已知,点![]() 是等边
是等边![]() 内的任一点,连接
内的任一点,连接![]() ,
,![]() ,
,![]() .
.
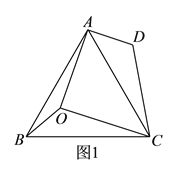
如图![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,使
,使![]() 与
与![]() 重合,得
重合,得![]() .
.
(![]() )
)![]() 的度数是__________.
的度数是__________.
(![]() )用等式表示线段
)用等式表示线段![]() ,
,![]() ,
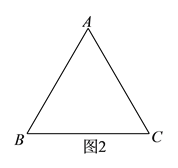
,![]() 之间的数量关系,并证明.(图
之间的数量关系,并证明.(图![]() 为备用图)
为备用图)
参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,证明见解析.
,证明见解析.
【解析】试题分析:
(1)由已知条件易得∠AOC=360°-150°-120°=90°,由旋转的性质易得:∠ADC=∠BOC=120°,∠DCO=60°,结合四边形的内角和为360°即可得到∠DAO=360°-90°-60°-120°=90°;
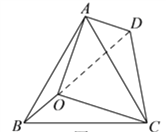
(2)如图3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,由旋转的性质可知AD=BO,CD=CO,∠OCD=60°,由此可得△OCD是等边三角形,从而可得OC=OD,结合(1)中结论∠DAO=90°由勾股定理即可得到:OB2+OA2=OC2.
试题解析:
(1)∵△ADC是由△BOC绕点C顺时针旋转60°得到的,
∴∠ADC=∠BOC=120°,∠DCO=60°,
又∵∠AOC=360°-∠AOB-∠BOC=360°-150°-120°=90°,
∴在四边形AOCD中,∠DAO=360°-120°-60°-90°=90°;
(![]() )
)![]() .理由如下:
.理由如下:
如图3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,由旋转的性质可知AD=BO,CD=CO,∠OCD=60°,
∴△OCD是等边三角形,
∴OC=OD,
由(1)可知∠DAO=90°,
∴在Rt△DAO中,![]() ,
,
∴OA2+OB2=OC2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验与探究:
(
 )由图观察易知
)由图观察易知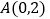 关于直线
关于直线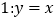 的对称点
的对称点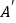 的坐标为
的坐标为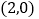 ,请在图中分别标明
,请在图中分别标明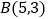 、
、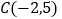 关于直线
关于直线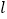 的对称点
的对称点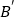 、
、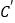 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: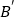 __________、
__________、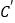 __________.
__________.归纳与发现:
(
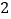 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点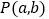 关于第一、三象限的角平分线
关于第一、三象限的角平分线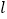 的对称点
的对称点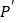 的坐标为__________(不必证明).
的坐标为__________(不必证明).运用与拓广:
(
 )已知两点
)已知两点 、
、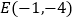 ,试在直线
,试在直线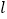 上确定一点
上确定一点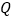 ,使点
,使点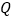 到
到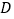 、
、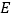 两点的距离之和最小,并求出
两点的距离之和最小,并求出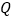 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知长方形
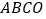 ,
,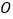 为坐标原点,
为坐标原点,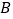 点坐标为
点坐标为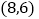 ,
,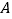 点在
点在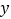 轴的正半轴上,
轴的正半轴上,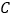 点在
点在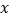 轴的正半轴上,
轴的正半轴上,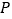 是线段
是线段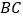 上的动点,设
上的动点,设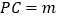 ,已知点
,已知点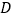 在第一象限且是直线
在第一象限且是直线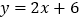 上一点,若
上一点,若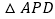 是等腰直角三角形.
是等腰直角三角形.(
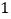 )求点
)求点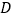 的坐标并写出解题过程.
的坐标并写出解题过程.(
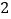 )直角
)直角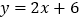 向下平移
向下平移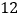 个单位后,在该直线上是否存在点
个单位后,在该直线上是否存在点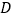 ,使
,使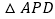 是等腰直角三角形.
是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )

A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
-
科目: 来源: 题型:
查看答案和解析>>【题目】冬季即将来临,是流感的高发期,某中学积极进行班级环境消毒,总务处购买甲、乙两种消毒液共100瓶,购买这两种消毒液共用780元,其中甲种消毒液共用240元,且乙种消毒液的单价是甲种消毒液单价的1.5倍.
(1)求甲、乙两种消毒液的单价各为多少元?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),共140瓶,且所需费用不超过1210元,问甲种消毒液至少要购买多少瓶?
相关试题

