【题目】如图,在矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD是位似图形且相似比为![]() ,求C,F之间的距离.
,求C,F之间的距离.

参考答案:
【答案】C,F之间的距离为![]()
【解析】试题分析:
如图,过点F作FH⊥BC于点H,连接CF,由已知容易求得EF=4,AE=6,从而可得CH=BC-BH=BC-EF=2,FH=BE=AB-AE=3,这样在Rt△CHF中,由勾股定理即可求得CF=![]() .
.
试题解析:
如图,过点F作FH⊥BC于点H,连接CF,
∴∠BHF=∠CFH=90°,
∵矩形AEFG与矩形ABCD是位似图形且相似比为![]() ,AB=9,BC=6,
,AB=9,BC=6,
∴∠B=∠BEF=90°,AE=6,EF=4,
∴四边形BEFH是矩形,
∴BH=EF=4,FH=BE=AB-AE=3,
∴CH=BC-BH=6-4=2,
∴在Rt△CFH中,CF=![]() ,即点C和点F之间的距离为
,即点C和点F之间的距离为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6m 长的圆钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪长为 0.8m 的用料时,最多可剪 根;
方法②:当先剪下 1 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根;
方法③:当先剪下 2 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根.
(2)分别用(1)中的方法②和方法③各裁剪多少根 6m 长的钢管,才能刚好得到所需要的相应数量的材料?
(3)试探究:除(2)中方案外,在(1)中还有哪两种方法联合,所需要 6m 长的钢管与(2) 中根数相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
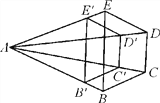
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若
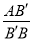 =3,S四边形BCDE=20,求S四边形B′C′D′E′.
=3,S四边形BCDE=20,求S四边形B′C′D′E′. -
科目: 来源: 题型:
查看答案和解析>>【题目】若正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…在直线l上,直线l与x轴的夹角为45°和点C1,C2,C3,…在x轴上,已知点A1 (0,1),则A2018的坐标是( ).

A.
 B.
B. 
C.
 D.
D. 
相关试题

