【题目】如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
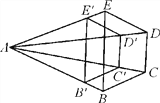
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若![]() =3,S四边形BCDE=20,求S四边形B′C′D′E′.
=3,S四边形BCDE=20,求S四边形B′C′D′E′.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由已知条件易得: ![]() ,结合四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,即可得到两个四边形是位似图形的结论;
,结合四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,即可得到两个四边形是位似图形的结论;
(2)由![]() 可得
可得![]() ,结合四边形B′C′D′E′和BCDE是位似图形即可得到:四边形B′C′D′E′和BCDE的相似比为
,结合四边形B′C′D′E′和BCDE是位似图形即可得到:四边形B′C′D′E′和BCDE的相似比为![]() ,结合S四边形BCDE=20,即可求得S四边形B′C′D′E′=
,结合S四边形BCDE=20,即可求得S四边形B′C′D′E′=![]() .
.
试题解析:
(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴![]() ,
,
又∵四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,
∴四边形B′C′D′E′和BCDE是位似图形;
(2)∵![]() ,
,
∴![]() ,
,
又∵四边形B′C′D′E′和BCDE是位似图形,
∴四边形B′C′D′E′和BCDE的相似比为![]() ,
,
∴S四边形B′C′D′E′:S四边形BCDE=9:16,
又∵S四边形BCDE=20,
∴S四边形B′C′D′E′=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD是位似图形且相似比为
 ,求C,F之间的距离.
,求C,F之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…在直线l上,直线l与x轴的夹角为45°和点C1,C2,C3,…在x轴上,已知点A1 (0,1),则A2018的坐标是( ).

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有_____填序号)
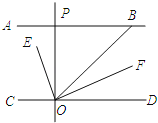
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x与双曲线y=
x与双曲线y= (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y= (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A. 3 B. 6 C.
 D.
D. 
相关试题

