【题目】小明家需要用钢管做防盗窗,按设计要求,其中需要长为 0.8m,2.5m 且粗细相同的钢管分别为 100 根,32 根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为 6m.
(1)试问一根 6m 长的圆钢管有哪些裁剪方法呢?请填写下空(余料作废).
方法①:当只裁剪长为 0.8m 的用料时,最多可剪 根;
方法②:当先剪下 1 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根;
方法③:当先剪下 2 根 2.5m 的用料时,余下部分最多能剪 0.8m 长的用料 根.
(2)分别用(1)中的方法②和方法③各裁剪多少根 6m 长的钢管,才能刚好得到所需要的相应数量的材料?
(3)试探究:除(2)中方案外,在(1)中还有哪两种方法联合,所需要 6m 长的钢管与(2) 中根数相同?
参考答案:
【答案】(1)①7; ②4;③1;(2)用方法②剪24根,方法③裁剪4根6m长的钢管;(3)方法①与方法③联合,所需要6m长的钢管与(2)中根数相同.
【解析】
第一问根据题目说的做,
第二问设方程,设用方法②剪x根,方法③裁剪y根6m长的钢管,即可得到二元一次方程组,求解方程即可
第三问设方程,设方法①裁剪m根,方法③裁剪n根6m长的钢管,即可得到二元一次方程组,求解方程即可
(1)①6÷0.8=7…0.4,因此当只裁剪长为0.8m的用料时,最多可剪7根;
②(6-2.5)÷0.8=4…0.3,因此当先剪下1根2.5m的用料时,余下部分最多能剪0.8m长的用料4根;
③(6-2.5×2)÷0.8=1…0.2,因此当先剪下2根2.5m的用料时,余下部分最多能剪0.8m长的用料1根;
故答案为7,4,1.
(2)设用方法②剪x根,方法③裁剪y根6m长的钢管,由题意,得
![]()
解得: ![]()
答:用方法②剪24根,方法③裁剪4根6m长的钢管;
(3)设方法①裁剪m根,方法③裁剪n根6m长的钢管,由题意,得
![]()
解得: ![]()
∴m+n=28.
∵x+y=24+4=28,
∴m+n=x+y.
设方法①裁剪a根,方法②裁剪b根6m长的钢管,由题意,得
![]()
解得: ![]() 无意义.
无意义.
∴方法①与方法③联合,所需要6m长的钢管与(2)中根数相同.
-
科目: 来源: 题型:
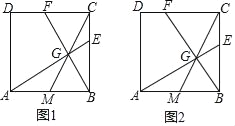
查看答案和解析>>【题目】已知正方形ABCD,点M为边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(-2,1),B(-3,-2),C(1,-2).把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
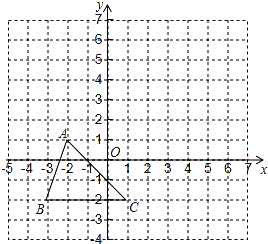
(1)在图中画出△A′B′C′,并写出点A′,B′,C′的坐标;
(2)连接A′C和A′A,求三角形AA′C的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享经济与我们的生活息息相关,其中,共享单车的使用给我们的生活带来了很多便利,但在使用过程中出现一些不文明现象.某市记者为了解“使用共享单车时的不文明行为”,随机抽查了该市部分市民,并对调查结果进行了整理,绘制了如下两幅尚不完整的统计图表(每个市民仅持有一种观点).

请根据以上信息,解答下列问题:
(1)填空: a= ; b= ; m= ;
(2)求扇形图中B组所在扇形的圆心角度数;
(3)若该市约有100万人,请你估计其中持有D组观点的市民人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=9,BC=6,若矩形AEFG与矩形ABCD是位似图形且相似比为
 ,求C,F之间的距离.
,求C,F之间的距离.
相关试题

