【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上两点,
上两点,![]() ,过点
,过点![]() 作
作![]() ,且点
,且点![]() 为边
为边![]() 延长线上一点.
延长线上一点.
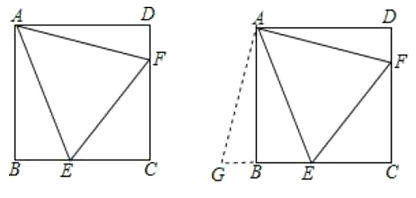
(1)![]() 吗?说明理由.
吗?说明理由.
(2)若线段![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
参考答案:
【答案】(1)见解析;(2)12;(3)EF=10
【解析】
(1)通过正方形的性质可得AB=AD、∠ABG =∠D,即可证明△GAB≌△FAD.
(2)通过证明△GAE≌△FAE(SAS)和△GAB≌△FAD,可得EF=GE和GB=DF,从而可得EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4,根据EC=BCBE可得EC=12(x4)=16x,根据勾股定理列方程求解即可.
(1)全等.
证明:∵四边形ABCD为正方形
∴AB=AD,∠ABE=∠D=90![]() ,
,
∴∠ABG =90![]() =∠D
=∠D
在△ABG和△ADF中,
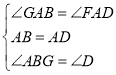
∴△GAB≌△FAD.
(2)∵∠BAD=90![]() ,∠EAF=45
,∠EAF=45![]()
∴∠DAF+∠BAE=45![]()
∵△GAB≌△FAD
∴∠GAB=∠FAD,AG=AF
∴∠GAB+∠BAE=45![]()
∴∠GAE=45
∴∠GAE=∠EAF
在△GAE和△FAE中
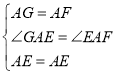
∴△GAE≌△FAE(SAS)
∴EF=GE.
∵△GAB≌△FAD
∴GB=DF
∴EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4.
∵EC=BCBE,
∴EC=12(x4)=16x.
在Rt△EFC中,依据勾股定理可知:
EF2=FC2+EC2,
即(16x) 2+82=x2,
解得:x=10.
∴EF=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
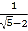 ,y=
,y=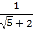
(1)求x2+xy+y2.
(2)若x的小数部分为a,y的整数部分为b,求ax+by的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
(1)求点B、点D的坐标,
(2)判断△ACD的形状,并求出△ACD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
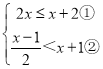
请结合题意填空,完成本题解答:
(1)解不等式①,得______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BD是△ABC的角平分线,ED⊥BC,∠BAC=90°,∠C=30°.

(1)求证:CE=BE;
(2)若AD=3,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
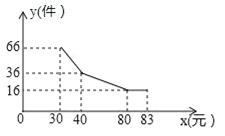
(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
相关试题

