【题目】已知BD是△ABC的角平分线,ED⊥BC,∠BAC=90°,∠C=30°.

(1)求证:CE=BE;
(2)若AD=3,求△ABC的面积.
参考答案:
【答案】(1)见解析;(2)△ABC的面积=![]() .
.
【解析】
(1)根据直角三角形的性质和角平分线的定义证出∠C=∠DBC,然后根据等角对等边即可证出DC=DB,然后利用三线合一即可得出结论;
(2)利用30°所对的直角边是斜边的一半即可求出BD和AB,从而求出AC,然后根据三角形的面积公式计算即可.
(1)证明:∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠DBC=![]() ∠ABC=30°,
∠ABC=30°,
∴∠C=∠DBC,
∴DC=DB,
∵DE⊥BC,
∴EC=BE.
(2)解:在Rt△ABD中,∵∠A=90°,AD=3,∠ABD=30°,
∴BD=2AD=6,AB=![]() =3
=3![]() ,
,
∴DB=DC=6,
∴AC=9,
∴△ABC的面积=![]() ×
×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
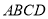 中,点
中,点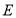 、
、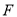 分别为边
分别为边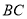 、
、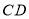 上两点,
上两点,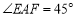 ,过点
,过点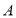 作
作 ,且点
,且点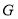 为边
为边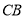 延长线上一点.
延长线上一点.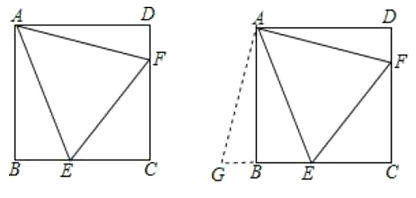
(1)
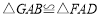 吗?说明理由.
吗?说明理由.(2)若线段
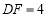 ,
,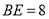 ,求线段
,求线段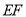 的长度.
的长度.(3)若
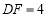 ,
,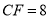 ,求线段
,求线段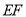 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
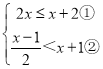
请结合题意填空,完成本题解答:
(1)解不等式①,得______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来;
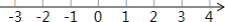
(4)原不等式组的解集为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
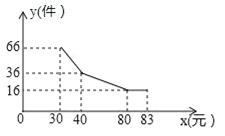
(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C.
(1)求抛物线的解析式;
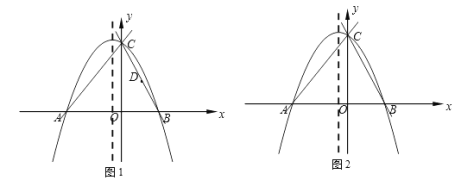
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线y=ax+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
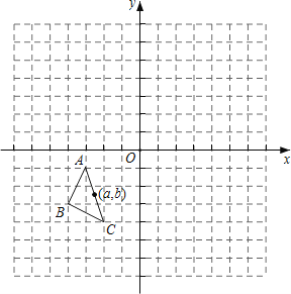
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
相关试题

