【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求: 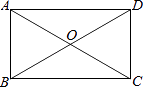
(1)AB的长;
(2)矩形ABCD的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是矩形,
∴OB=OC,∠ABC=90°,
又∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴AB= ![]() AC=
AC= ![]() ×6=3
×6=3
(2)解:∵AB2+BC2=AC2,
∴BC= ![]() =3
=3 ![]() ,
,
∴矩形ABCD的面积=AB×BC=3×3 ![]() =9
=9 ![]()
【解析】(1)根据OB=OC,∠ABC=90°,以及∠BOC=120°,可得出∠OBC=∠OCB=30°,进而得到AB= ![]() AC=3;(2)根据勾股定理即可得出BC=
AC=3;(2)根据勾股定理即可得出BC= ![]() =3
=3 ![]() ,进而得出矩形ABCD的面积.
,进而得出矩形ABCD的面积.
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a﹣2a=1B.a2+a5=a7C.a2a4=a6D.(ab)3=ab3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
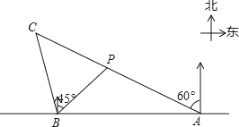
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点
中,点 在边
在边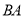 上,
上, 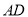 ⊥
⊥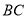 ,
, 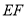 ⊥
⊥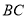 ,垂足分别是
,垂足分别是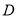 、
、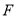 ,∠1=∠2.
,∠1=∠2.(1)
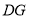 与
与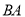 平行吗?为什么?
平行吗?为什么?(2)若∠
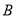 =51°,∠
=51°,∠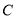 =54°,求∠
=54°,求∠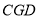 的度数.
的度数.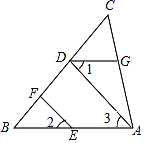
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.

(1)求证:四边形CEDF是平行四边形;
(2)①当AE=cm时,四边形CEDF是矩形; ②当AE=cm时,四边形CEDF是菱形.
(直接写出答案,不需要说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点
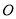 为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径
为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径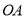 表示时针,半径
表示时针,半径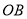 表示分针,它们所成的钟面角为∠
表示分针,它们所成的钟面角为∠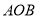 ;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.
;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.(1)时针每分钟转动的角度为 °,分针每分钟转动的角度为 °;
(2)8点整,钟面角∠
 = °,钟面角与此相等的整点还有: 点;
= °,钟面角与此相等的整点还有: 点;(3)如图,设半径
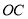 指向12点方向,在图中画出6点15分时半径
指向12点方向,在图中画出6点15分时半径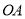 、
、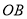 的大概位置,并求出此时∠
的大概位置,并求出此时∠ 的度数.
的度数.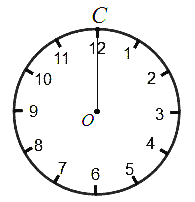
相关试题

