【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
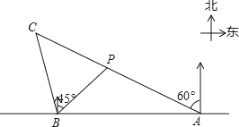
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
参考答案:
【答案】(1)点P到海岸线l的距离为(![]() ﹣1)km;(2)点C与点B之间的距离为
﹣1)km;(2)点C与点B之间的距离为![]() km.
km.
【解析】试题分析:(1)过点P作PD⊥AB于点D,设PD=xkm,先解Rt△PBD,用含x的代数式表示BD,再解Rt△PAD,用含x的代数式表示AD,然后根据BD+AD=AB,列出关于x的方程,解方程即可;(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=![]() AB=1km,再解Rt△BCF,得出BC=
AB=1km,再解Rt△BCF,得出BC=![]() BF=
BF=![]() km.
km.
试题解析:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
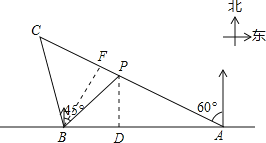
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=![]() PD=
PD=![]() xkm.
xkm.
∵BD+AD=AB,
∴x+![]() x=2,x=
x=2,x=![]() ﹣1,
﹣1,
∴点P到海岸线l的距离为(![]() ﹣1)km;
﹣1)km;
(2)如图,过点B作BF⊥AC于点F.根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=![]() AB=1km.
AB=1km.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=![]() BF=
BF=![]() km,
km,
∴点C与点B之间的距离为![]() km.
km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠
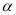 是锐角,∠
是锐角,∠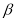 是钝角,且∠
是钝角,且∠ +∠
+∠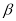 =180°,那么下列结论正确的是( )
=180°,那么下列结论正确的是( )A. ∠
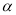 的补角和∠
的补角和∠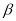 的补角相等 B. ∠
的补角相等 B. ∠ 的余角和∠
的余角和∠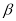 的补角相等
的补角相等C. ∠
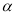 的余角和∠
的余角和∠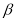 的补角互余 D. ∠
的补角互余 D. ∠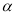 的余角和∠
的余角和∠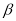 的补角互补
的补角互补 -
科目: 来源: 题型:
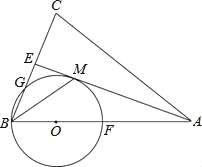
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)当BC=8,AC=12时,求⊙O的半径.
(3)在(2)的条件下,求线段BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a﹣2a=1B.a2+a5=a7C.a2a4=a6D.(ab)3=ab3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:
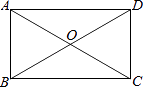
(1)AB的长;
(2)矩形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点
中,点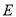 在边
在边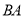 上,
上, 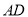 ⊥
⊥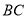 ,
, 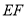 ⊥
⊥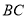 ,垂足分别是
,垂足分别是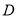 、
、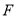 ,∠1=∠2.
,∠1=∠2.(1)
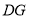 与
与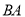 平行吗?为什么?
平行吗?为什么?(2)若∠
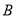 =51°,∠
=51°,∠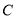 =54°,求∠
=54°,求∠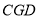 的度数.
的度数.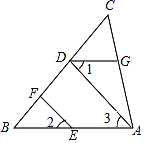
相关试题

