【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF. 
(1)求证:四边形CEDF是平行四边形;
(2)①当AE=cm时,四边形CEDF是矩形; ②当AE=cm时,四边形CEDF是菱形.
(直接写出答案,不需要说明理由)
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCG=∠EDG,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
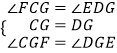 ,
,
∴△FCG≌△EDG(ASA)
∴FG=EG,
∵CG=DG,
∴四边形CEDF是平行四边形;
(2)3.5;2
【解析】(2)①解:当AE=3.5时,平行四边形CEDF是矩形, 理由是:过A作AM⊥BC于M,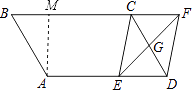
∵∠B=60°,AB=3,
∴BM=1.5,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=3,BC=AD=5,
∵AE=3.5,
∴DE=1.5=BM,
在△MBA和△EDC中,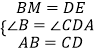 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:3.5;
②当AE=2时,四边形CEDF是菱形,
理由是:∵AD=5,AE=2,
∴DE=3,
∵CD=3,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:2.
(1)证△CFG≌△EDG,推出FG=EG,根据平行四边形的判定推出即可;(2)①求出△MBA≌△EDC,推出∠CED=∠AMB=90°,根据矩形的判定推出即可;
②求出△CDE是等边三角形,推出CE=DE,根据菱形的判定推出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求:
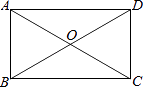
(1)AB的长;
(2)矩形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
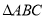 中,点
中,点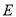 在边
在边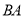 上,
上, 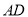 ⊥
⊥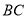 ,
, 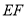 ⊥
⊥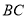 ,垂足分别是
,垂足分别是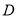 、
、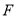 ,∠1=∠2.
,∠1=∠2.(1)
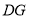 与
与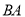 平行吗?为什么?
平行吗?为什么?(2)若∠
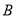 =51°,∠
=51°,∠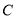 =54°,求∠
=54°,求∠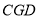 的度数.
的度数.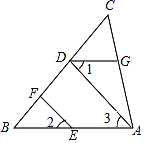
-
科目: 来源: 题型:
查看答案和解析>>【题目】钟面角是指时钟的时针与分针所成的角.如图,在钟面上,点
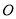 为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径
为钟面的圆心,图中的圆我们称之为钟面圆. 为便于研究,我们规定: 钟面圆的半径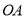 表示时针,半径
表示时针,半径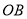 表示分针,它们所成的钟面角为∠
表示分针,它们所成的钟面角为∠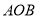 ;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.
;本题中所提到的角都不小于0°,且不大于180°;本题中所指的时刻都介于0点整到12点整之间.(1)时针每分钟转动的角度为 °,分针每分钟转动的角度为 °;
(2)8点整,钟面角∠
 = °,钟面角与此相等的整点还有: 点;
= °,钟面角与此相等的整点还有: 点;(3)如图,设半径
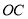 指向12点方向,在图中画出6点15分时半径
指向12点方向,在图中画出6点15分时半径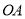 、
、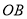 的大概位置,并求出此时∠
的大概位置,并求出此时∠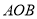 的度数.
的度数.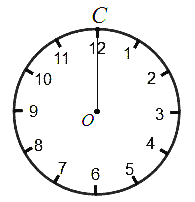
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个仓库共存有粮食60
 .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:(1)甲仓库运进粮食14
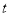 ,乙仓库运出粮食10
,乙仓库运出粮食10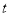 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?(2)如果甲仓库原有的粮食比乙仓库的2倍少3
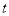 ,则甲仓库运出多少
,则甲仓库运出多少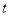 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等? (3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1
 ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】将点A先向下平移3个单位长度,再向右平移4个单位长度,得到点A'(-3,-6),则点A的坐标为( )
A. (-7,3)B. (6,-10)C. (-7,-3)D. (-1,-10)
相关试题

