【题目】已知二次函数y=x2﹣2mx+m2+m+1的图象与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图象关于x轴翻折,所得图象的顶点为D,若CD=8.求四边形ACBD的面积.
参考答案:
【答案】
(1)解:∵二次函数图象与x轴有两个交点,
∴△=4m2﹣4(m2+m+1)=﹣4m﹣4>0,
∴m<﹣1;
(2)解:y=x2﹣2m x+m2+m+1=(x﹣m) 2+m+1,
∵CD=8,
∴m+1=﹣4,解得m=﹣5,
∴y=x2+10 x+21,
令y=0,x2+10 x+21=0,解得x1=﹣3,x2=﹣7,则A(﹣3,0),B(﹣7,0)
∴AB=4,
∴S四边形ACBD=2× ![]() ×4×4=16.
×4×4=16.
【解析】(1)根据判别式的意义得到△=4m2﹣4(m2+m+1)=﹣4m﹣4>0,然后解不等式即可;(2)先配方得到y=(x﹣m) 2+m+1,则顶点的纵坐标为m+1,利用C点和D点关于x轴对称得到m+1=﹣4,解得m=﹣5,所以y=x2+10 x+21,然后解方程x2+10 x+21=0得到A(﹣3,0),B(﹣7,0),再利用三角形面积公式计算四边形ACBD的面积.
【考点精析】解答此题的关键在于理解二次函数图象的平移的相关知识,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
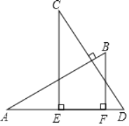
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
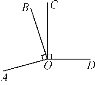
查看答案和解析>>【题目】(1)如图,已知∠AOB=∠COD=90°,试写出两个与图①中角(直角除外)有关的结论:
(ⅰ)∠__ __=∠__ __,
(ⅱ)∠__ __+∠__ __=180°;
(2)请选择(1)中的一个结论说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离. (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.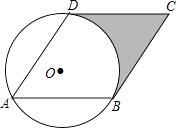
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值
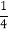 x2+2(x-
x2+2(x- y2)-
y2)- (-3x2+2y2)-
(-3x2+2y2)- x,其中x=2,y=-3;
x,其中x=2,y=-3;(2)已知A=2a2-a,B=-5a+1.
①化简:3A-2B+2;
②当a=-
 时,求3A-2B+2的值.
时,求3A-2B+2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB的延长线上,AC=
 BC,D在AB的反向延长线上,BD=
BC,D在AB的反向延长线上,BD=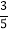 DC.
DC.(1)在图上画出点C和点D的位置;
(2)设线段AB长为x,则BC=__ __,AD=__ __;(用含x的代数式表示)
(3)设AB=12 cm,求线段CD的长.

相关试题

