【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°.求小岛B到河边公路AD的距离. (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
参考答案:
【答案】解:过B作BE⊥CD垂足为E, 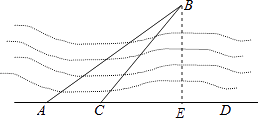
设BE=x米,
在Rt△ABE中,tanA= ![]() ,
,
AE= ![]() =
= ![]() =
= ![]() x,
x,
在Rt△ABE中,tan∠BCD= ![]() ,
,
CE= ![]() =
= ![]() =x,
=x,
AC=AE﹣CE,![]() x﹣x=150,
x﹣x=150,
x=450.
答:小岛B到河边公路AD的距离为450米.
【解析】过B作BE⊥CD垂足为E,设BE=x米,再利用锐角三角函数关系得出AE= ![]() x,CE=x,根据AC=AE﹣CE,得到关于x的方程,即可得出答案.
x,CE=x,根据AC=AE﹣CE,得到关于x的方程,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
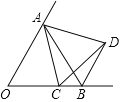
A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
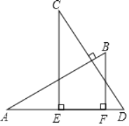
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
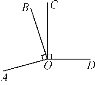
查看答案和解析>>【题目】(1)如图,已知∠AOB=∠COD=90°,试写出两个与图①中角(直角除外)有关的结论:
(ⅰ)∠__ __=∠__ __,
(ⅱ)∠__ __+∠__ __=180°;
(2)请选择(1)中的一个结论说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2mx+m2+m+1的图象与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图象关于x轴翻折,所得图象的顶点为D,若CD=8.求四边形ACBD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.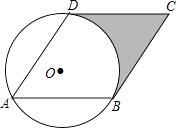
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值
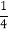 x2+2(x-
x2+2(x- y2)-
y2)- (-3x2+2y2)-
(-3x2+2y2)- x,其中x=2,y=-3;
x,其中x=2,y=-3;(2)已知A=2a2-a,B=-5a+1.
①化简:3A-2B+2;
②当a=-
 时,求3A-2B+2的值.
时,求3A-2B+2的值.
相关试题

