【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=![]() AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
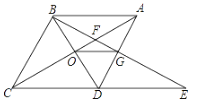
A. ①③B. ①③④C. ①②③D. ②②④
参考答案:
【答案】A
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=
AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
解:四边形ABCD是菱形,
在△ABG和△DEG中,

∴△ABG≌△DEG(AAS),
∴.AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB//CE,AB=DE,
∴四边形ABDE是平行四边形,
∴∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,③正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,

∴△ABG≌△DCO
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,则②不正确。
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴ S四边形ODGF=S△ABF;④不正确;
故答案为:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(
 ,0),有下列结论:
,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-bm≥(am-b);其中所有正确的结论有( )个.
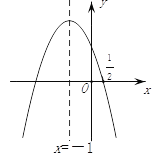
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:

(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.

-
科目: 来源: 题型:
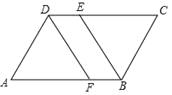
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为非零的实数,则
 的可能值的个数为( )
的可能值的个数为( )A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图矩形
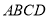 的对角线
的对角线 .
. 交于点
交于点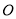 ,过点
,过点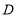 作
作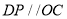 ,且
,且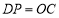 ,连接
,连接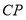 ,判断四边形
,判断四边形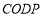 的形状并说明理由.
的形状并说明理由.(2)如果题目中的矩形变为菱形,四边形
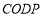 的形状____________.
的形状____________.(3)如果题目中的矩形变为正方形,四边形
 的形状____________.
的形状____________.
相关试题

