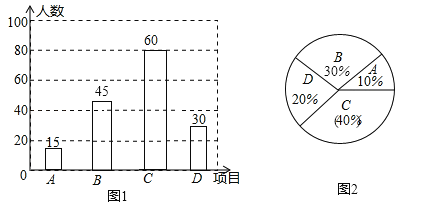
【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:

(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
参考答案:
【答案】(1)40%;(2)![]() .
.
【解析】
试题分析:(1)用A类的人数除以它所占百分比得到调查的总人数,然后用总人数分别减去其它各组人数可得C类人数,用C类人数除以总人数得到C类所占百分比,再补全统计图;
(2)画树状图展示所有6种等可能的结果数,再找出一男生一女生的结果数,然后根据概率公式求解.
试题解析:(1)调查的纵人数=15÷10%=150,所以喜欢“跑步”的学生人数=150﹣15﹣45﹣30=60(人),它所占的百分比=![]() ×100%=40%;
×100%=40%;
如图:
(2)画树状图为:
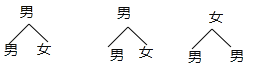
共有6种等可能的结果数,其中一男生一女生的结果数为4,所以刚好抽到一男生一女生的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线
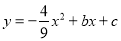 经过点A、C,与AB交于点D.
经过点A、C,与AB交于点D.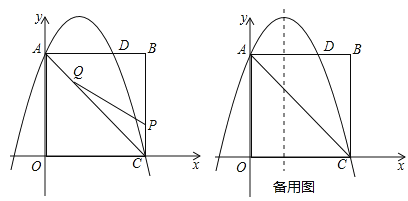
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线
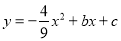 的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】写出“同位角相等,两直线平行”的题设为 , 结论为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
A. 2500(1+x)2=3200 B. 2500(1+2x)=3200
C. 3200(1-x)2=2500 D. 3200(1-2x)=2500
-
科目: 来源: 题型:
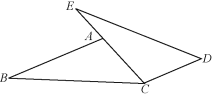
查看答案和解析>>【题目】(1)已知:如图,点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.求证:BC=ED.
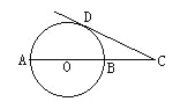
(2)如图,在⊙O中,过直径AB延长线上的点C做⊙O的一条切线,切点为D,若CD=4,CB=2.求:⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体的顶点数、面数和棱数分别是( )
A. 8、6、12 B. 6、8、12 C. 8、12、6 D. 6、8、10
-
科目: 来源: 题型:
查看答案和解析>>【题目】在算式( )+6=-8中,括号里应填( )
A. 2 B. -2 C. 14 D. -14
相关试题

