【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】
(1)证明:连接CD,
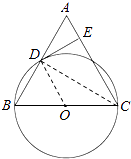
∵BC为⊙O的直径,∴CD⊥AB,
又∵AC=BC,
∴AD=BD,即点D是AB的中点
(2)解:DE是⊙O的切线.
证明:连接OD,则DO是△ABC的中位线,
∴DO∥AC,
又∵DE⊥AC,
∴DE⊥DO即DE是⊙O的切线
(3)解:∵AC=BC,∴∠B=∠A,
∴cosB=cosA= ![]() ,
,
∵cosB= ![]() ,BC=18,
,BC=18,
∴BD=6,
∴AD=6,
∵cosA= ![]() ,
,
∴AE=2,
在Rt△AED中,DE= ![]() .
.
【解析】(1)连接CD,利用圆周角定理得出CD⊥AB,又由等腰三角形的三线合一得出点D是AB的中点;(2)连接OD,则DO是△ABC的中位线,利用中位线定理得DO∥AC,又因DE⊥AC从而得出DE⊥DO,进而得出结论;(3)根据余弦的定义得出BD的长度,从而得出AD的长度,再根据等角的余弦相等得出AE的长度,最后用勾股定理得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=
 ,求AB的长.
,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,点
 是等腰三角形
是等腰三角形 的底边
的底边 上的一个动点,过点
上的一个动点,过点 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,请观察
,请观察 与
与 ,它们有何数量关系?并证明你的猜想.
,它们有何数量关系?并证明你的猜想.(2)如果点
 沿着底边
沿着底边 所在的直线,按由
所在的直线,按由 向
向 的方向运动到
的方向运动到 的延长线上时,(1)中所得的结论还成立吗?请你在图2中完成图形,写出结论.并证明你的猜想.
的延长线上时,(1)中所得的结论还成立吗?请你在图2中完成图形,写出结论.并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 满足
满足 .将线段
.将线段 先向上平移2个单位,再向右平移1个单位后得到线段
先向上平移2个单位,再向右平移1个单位后得到线段 ,并连接
,并连接 .
.
(1)请求出点
 和点
和点 的坐标;
的坐标;(2)点
 从
从 点出发,以每秒1个单位的速度向上平移运动.设运动时间为
点出发,以每秒1个单位的速度向上平移运动.设运动时间为 秒,问:是否存在这样的
秒,问:是否存在这样的 ,使得四边形
,使得四边形 的面积等于8?若存在,请求出
的面积等于8?若存在,请求出 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;(3)在(2)的条件下,点
 从
从 点出发的同时,点
点出发的同时,点 从点
从点 出发,以每秒2个单位的速度向左平移运动,设射线
出发,以每秒2个单位的速度向左平移运动,设射线 交
交 轴于点
轴于点 .设运动时间为
.设运动时间为 秒,问:
秒,问: 的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:已知
 中,
中, ,在
,在 内部作
内部作 分别交
分别交 于点
于点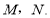

[操作](1)将
 绕点
绕点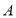 逆时针旋转
逆时针旋转 ,使
,使 边与
边与 边重合,把旋转后点
边重合,把旋转后点 的对应点记作点
的对应点记作点 ,得到
,得到 ,请在图中画出
,请在图中画出 ;(不写出画法)
;(不写出画法)[探究](2)在
 作图的基础上,连接
作图的基础上,连接 , 求证:
, 求证: 
[拓展](3)写出线段
 和
和 之间满足的数量关系,并简要说明理由.
之间满足的数量关系,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).

(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店卖出甲型号手机10台和乙型号手机12台后的销售额为
 万元;卖出甲型号手机6台和乙型号手机9台后的销售额为
万元;卖出甲型号手机6台和乙型号手机9台后的销售额为 万元.
万元.(1)请问甲型号手机和乙型号手机每台售价为多少元?
(2)若甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于
 万元且不少于
万元且不少于 万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润.
万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润.
相关试题

