【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
参考答案:
【答案】
(1)解:假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10﹣t=2t,
解得t= ![]() ,
,
∴当t= ![]() s时,四边形PQCM是平行四边形
s时,四边形PQCM是平行四边形
(2)解:∵PQ∥AC, 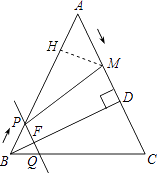
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得BF= ![]() t,
t,
∴FD=BD﹣BF=8﹣ ![]() t,
t,
又∵MC=AC﹣AM=10﹣2t,
∴y= ![]() (PQ+MC)FD=
(PQ+MC)FD= ![]() (t+10﹣2t)(8﹣
(t+10﹣2t)(8﹣ ![]() t)=
t)= ![]() t2﹣8t+40.
t2﹣8t+40.
【解析】(1)四边形PQCM是平行四边形,得它的对边平行,进而得到AP=AM,列出关于t的方程,解方程即可求出答案;(2)根据PQ∥AC,可得△PBQ∽△ABC,根据相似三角形形状相似知道△PBQ为等腰三角形,即PQ=PB=t,再由相似三角形对应高的比等于相似比,用含t的式子就可以表示出FD,AM,CM,最后根据提醒的面积公式就能找出函数关系式。
【考点精析】本题主要考查了函数关系式和等腰三角形的性质的相关知识点,需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 满足
满足 .将线段
.将线段 先向上平移2个单位,再向右平移1个单位后得到线段
先向上平移2个单位,再向右平移1个单位后得到线段 ,并连接
,并连接 .
.
(1)请求出点
 和点
和点 的坐标;
的坐标;(2)点
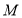 从
从 点出发,以每秒1个单位的速度向上平移运动.设运动时间为
点出发,以每秒1个单位的速度向上平移运动.设运动时间为 秒,问:是否存在这样的
秒,问:是否存在这样的 ,使得四边形
,使得四边形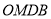 的面积等于8?若存在,请求出
的面积等于8?若存在,请求出 的值:若不存在,请说明理由;
的值:若不存在,请说明理由;(3)在(2)的条件下,点
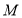 从
从 点出发的同时,点
点出发的同时,点 从点
从点 出发,以每秒2个单位的速度向左平移运动,设射线
出发,以每秒2个单位的速度向左平移运动,设射线 交
交 轴于点
轴于点 .设运动时间为
.设运动时间为 秒,问:
秒,问: 的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.

(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:已知
 中,
中, ,在
,在 内部作
内部作 分别交
分别交 于点
于点

[操作](1)将
 绕点
绕点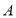 逆时针旋转
逆时针旋转 ,使
,使 边与
边与 边重合,把旋转后点
边重合,把旋转后点 的对应点记作点
的对应点记作点 ,得到
,得到 ,请在图中画出
,请在图中画出 ;(不写出画法)
;(不写出画法)[探究](2)在
 作图的基础上,连接
作图的基础上,连接 , 求证:
, 求证: 
[拓展](3)写出线段
 和
和 之间满足的数量关系,并简要说明理由.
之间满足的数量关系,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机店卖出甲型号手机10台和乙型号手机12台后的销售额为
 万元;卖出甲型号手机6台和乙型号手机9台后的销售额为
万元;卖出甲型号手机6台和乙型号手机9台后的销售额为 万元.
万元.(1)请问甲型号手机和乙型号手机每台售价为多少元?
(2)若甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于
 万元且不少于
万元且不少于 万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润.
万元的资金购进这两种手机共20台,请问有几种进货方案?若所有购进的手机都可以售出,请求出所有方案中的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系中,
 的顶点坐标分别
的顶点坐标分别 ,现将
,现将 先向右平移6个单位长度,再向下平移5个单位长度,得到
先向右平移6个单位长度,再向下平移5个单位长度,得到 .
.
(1)直接写出点
 的坐标;
的坐标;(2)在平面直角坐标中画出
 ,并求出
,并求出 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】自从新冠肺炎疫情爆发,我国高度重视并采取了强有力的措施进行防控,像钟南山爷爷和李兰娟奶奶等无数白衣天使为保卫大家的安全奋斗在抗疫一线. 武汉是疫情最先爆发的地区,“一方有难,八方支援”是中华传统美德,为了帮助武汉人民尽快度过难关,某校七年级全体同学参加了捐款活动.现随机抽查了部分同学捐款的情况统计如图所示:

(1)在本次调查中,一共抽查了_________名学生;
(2)请补全条形统计图,并计算在扇形统计图中,“捐款 20元”对应的圆心角度数是 度;
(3)在七年级600名学生中,捐款15元以上(不含15元)的学生估计有多少人?
相关试题

