【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数).
(1)讨论函数f(x)的单调性;
(2)若对任意的 ![]() ,都存在x0∈(0,1]使得不等式
,都存在x0∈(0,1]使得不等式 ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:由f(x)=lnx+x2﹣2ax+1,得 ![]() ,
,
令h(x)=2x2﹣2ax+1.
①当a≤0时,h(x)>0,则f'(x)>0成立,
△=4a2﹣8,当 ![]() 时,△≤0,则2x2﹣2ax+1≥0,h(x)≥0,即f'(x)≥0恒成立,
时,△≤0,则2x2﹣2ax+1≥0,h(x)≥0,即f'(x)≥0恒成立,
∴当 ![]() 时,f'(x)≥0,f(x)在(0,+∞)上单调递增;
时,f'(x)≥0,f(x)在(0,+∞)上单调递增;
②当 ![]() 时,由2x2﹣2ax+10≥0,得
时,由2x2﹣2ax+10≥0,得 ![]() 或
或 ![]() ,
,
由2x2﹣2ax+10<0,得 ![]() .
.
∴f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 单调递减;
单调递减;
(2)解:∵ ![]() ,
,
∴f'(x)>0,f(x)在(0,1]单调递增,f(x)max=f(1)=2﹣2a,
存在x0∈(0,1]使得不等式 ![]() 成立,
成立,
即2﹣2a+lna>m(a﹣a2),
∵任意的 ![]() ,∴a﹣a2<0,即
,∴a﹣a2<0,即 ![]() 恒成立,
恒成立,
令 ![]() ,则
,则 ![]() ,
,
∵任意的 ![]() ,
, ![]() ,
,
∴ ![]() 是增函数,
是增函数,
∴ ![]() ,
,
∵ ![]() 恒成立,
恒成立,
∴实数m的取值范围 ![]() .
.
【解析】(1)求出原函数的导函数,当a≤0时,导函数恒大于0,然后利用二次函数的判别式对a分类讨论求出导函数在不同区间内的符号,得到原函数的单调性;(2)由(1)知, ![]() 时,函数f(x)在(0,1]上单调递增,求出函数在(0,1]上的最大值2﹣2a,把存在x0∈(0,1]使得不等式
时,函数f(x)在(0,1]上单调递增,求出函数在(0,1]上的最大值2﹣2a,把存在x0∈(0,1]使得不等式 ![]() 成立转化为2﹣2a+lna>m(a﹣a2),得到
成立转化为2﹣2a+lna>m(a﹣a2),得到 ![]() 恒成立,构造函数
恒成立,构造函数 ![]() ,求导可知为增函数,得其最大值,则实数m的取值范围可求.
,求导可知为增函数,得其最大值,则实数m的取值范围可求.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=
 ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组
频数
频率
[10,15)
10
0.25
[15,20)
25
n
[20,25)
m
p
[25,30)
2
0.05
合计
M
1

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1:
 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: 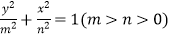 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 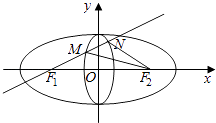
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程
 (α为参数) (Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标
(α为参数) (Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标  ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(Ⅱ)设点Q为曲线C上的一个动点,求它到直线l的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|+|x+a|,

(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)若a>﹣1,且当x∈[﹣a,1]时,不等式f(x)≤g(x)有解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
A. 钱
钱
B. 钱
钱
C.1钱
D. 钱
钱
相关试题

