【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.
参考答案:
【答案】
(1)解:由题可知 ![]() =0.25,
=0.25, ![]() =n,
=n, ![]() =p,
=p, ![]() =0.05.
=0.05.
又10+25+m+2=M,
解得M=40,n=0.625,m=3,p=0.075.
则[15,20)组的频率与组距之比a为0.125.
(2)解:参加社区服务的平均次数为:
![]() 次
次
(3)解:在样本中,处于[20,25)内的人数为3,可分别记为A,B,C,
处于[25,30]内的人数为2,可分别记为a,b.
从该5名学生中取出2人的取法有:
(A,a),(A,b),(B,a),(B,b),(C,a),(C,b),
(A,B),(A,C),(B,C),(a,b),共10种,
至少1人在[20,25)内的情况有共9种,
∴至少1人参加社区服务次数在区间[20,25)内的概率为 ![]() .
.
【解析】(1)由频率= ![]() ,能求出表中M、p及图中a的值.(2)由频数与频率的统计表和频率分布直方图能求出参加社区服务的平均次数.(3)在样本中,处于[20,25)内的人数为3,可分别记为A,B,C,处于[25,30]内的人数为2,可分别记为a,b,由此利用列举法能求出至少1人参加社区服务次数在区间[20,25)内的概率.
,能求出表中M、p及图中a的值.(2)由频数与频率的统计表和频率分布直方图能求出参加社区服务的平均次数.(3)在样本中,处于[20,25)内的人数为3,可分别记为A,B,C,处于[25,30]内的人数为2,可分别记为a,b,由此利用列举法能求出至少1人参加社区服务次数在区间[20,25)内的概率.
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.
-
科目: 来源: 题型:
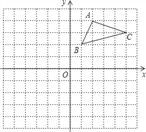
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ,a=2,
,a=2,  ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=
 ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1:
 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: 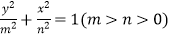 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 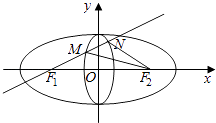
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数).
(1)讨论函数f(x)的单调性;
(2)若对任意的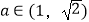 ,都存在x0∈(0,1]使得不等式
,都存在x0∈(0,1]使得不等式  成立,求实数m的取值范围.
成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程
 (α为参数) (Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标
(α为参数) (Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标  ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(Ⅱ)设点Q为曲线C上的一个动点,求它到直线l的距离的最小值.
相关试题

